Решение. Главное значение логарифмической функции имеет вид:
Главное значение логарифмической функции имеет вид:
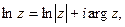 где область D:
где область D: 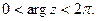
Действительная и мнимая части функции:
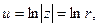
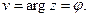
Проверим выполнимость условий КРЭДа. Для этого воспользуемся формулой (12), предварительно найдя частные производные:
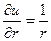 ;
; 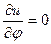 ;
; 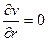 ;
; 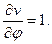 Подставим их в (12) и получим:
Подставим их в (12) и получим:
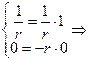 условия выполнены в любой точке области D, следовательно, функция дифференцируема в области D. И, очевидно, дифференцируемой в области D будет любая однозначная ветвь логарифма: Ln
условия выполнены в любой точке области D, следовательно, функция дифференцируема в области D. И, очевидно, дифференцируемой в области D будет любая однозначная ветвь логарифма: Ln 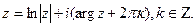
Найдем производную, используя формулу (13):
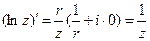 , как и было показано выше.
, как и было показано выше.
Определение 27.(первое определение аналитической функции)Функция 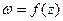 , дифференцируемая в каждой точке z области D и имеющая в этой области непрерывную производную
, дифференцируемая в каждой точке z области D и имеющая в этой области непрерывную производную 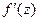 , называется аналитической в области D.
, называется аналитической в области D.
Замечание.Будем говорить, что 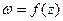 аналитическая в точке z области D, если
аналитическая в точке z области D, если 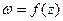 является аналитической в некоторой окрестности этой точки.
является аналитической в некоторой окрестности этой точки.
Другие названия аналитической функции: голоморфная, регулярная, моногенная.
Определение 28.Точки плоскости, в которых однозначная функция 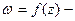 аналитическая, называются правильными точками.
аналитическая, называются правильными точками.
Определение 29.Точки, в которых нарушается аналитичность функции, называются особыми.
Пример 20. Найти особые точки функции 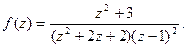
Дата добавления: 2015-07-14; просмотров: 556;
