Доказательство. По определению 25 функция называется дифференцируемой в точке z, если ее приращение можно записать в виде (9):
Необходимость.
По определению 25 функция 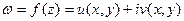 называется дифференцируемой в точке z, если ее приращение можно записать в виде (9):
называется дифференцируемой в точке z, если ее приращение можно записать в виде (9):

отсюда, выделив действительную 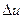 и мнимую
и мнимую 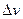 части функции
части функции 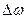 , получим:
, получим:
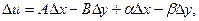
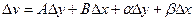 .
.
Данные равенства являются определениями дифференцируемости в точке функций двух переменных 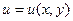 и
и 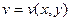 соответственно, где величины А и В не зависят от
соответственно, где величины А и В не зависят от 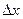 и
и 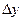 , а
, а 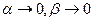 при
при 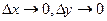 , причем для дифференцируемости функций
, причем для дифференцируемости функций 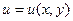 и
и 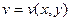 необходимо и достаточно, чтобы они имели в этой точке конечные производные, т.е. должны выполняться условия
необходимо и достаточно, чтобы они имели в этой точке конечные производные, т.е. должны выполняться условия 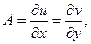
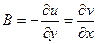 .
.
Достаточность.
Пусть функции 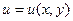 и
и 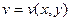 дифференцируемы, т.е. их приращения можно записать в виде
дифференцируемы, т.е. их приращения можно записать в виде 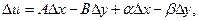
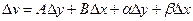 , где
, где 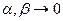 при
при 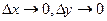 , A и B не зависят от
, A и B не зависят от 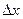 и
и 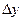 , причем
, причем 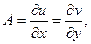
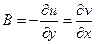 . Тогда
. Тогда
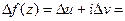
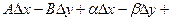
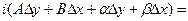
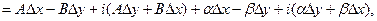
по формуле (9) это означает, что функция 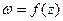 является дифференцируемой в точке z, что и требовалось доказать.
является дифференцируемой в точке z, что и требовалось доказать.
Следствие.Так какпроизводная дифференцируемой функции комплексного переменного равна 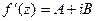 (по теореме 2), где
(по теореме 2), где 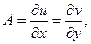
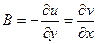 (по теореме 4), то она может быть найдена по одной из формул:
(по теореме 4), то она может быть найдена по одной из формул:
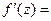
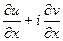 ,
, 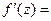
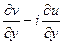 ,
, 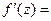
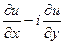 ,
, 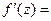
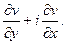 (11)
(11)
Замечание. Если введена полярная система координат, т.е. 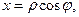
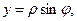 то условия КРЭДа имеют вид:
то условия КРЭДа имеют вид:
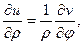
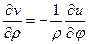 , (12)
, (12)
формулы для производной: 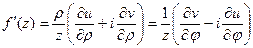 (13)
(13)
Остаются в силе все основные свойства производной и правила дифференцирования, выведенные для функций от вещественного переменного.
Теорема 5.Если функции f(z), g(z) дифференцируемы в точке z, то сумма, разность, произведение и частное этих функций также дифференцируемы в этой точке и имеют место формулы:
1) 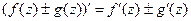 ; 2)
; 2) 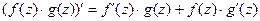 ;
;
3) 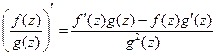 ,
, 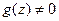 ;
;
4) если функция g(z) имеет производную в точке z, а функция f(g) имеет производную в соответствующей точке g, то сложная функция f(g(z))имеет производную в точке z и имеет место формула: 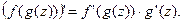
Применив условие (10) и одну из формул (11), можно вывести, что производные от элементарных функций комплексного переменного совпадают с производными от элементарных функций вещественного переменного:
( zа )' = а z а-1 ; ( е z )' = е z; ( а z )' = а z ln a;(ln z )' = 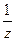 ; (sin z)' = cos z;(cos z)' = – sin z; ( tg z )' =
; (sin z)' = cos z;(cos z)' = – sin z; ( tg z )' = 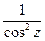 ; (arcsin z )' =
; (arcsin z )' = 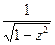 ;( arccos z )' =
;( arccos z )' = 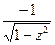 ; ( arctg z )' =
; ( arctg z )' = 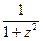 ; ( arcctg z ) =
; ( arcctg z ) = 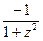 ; (sh z)' = ch z;(ch z)' = sh z.
; (sh z)' = ch z;(ch z)' = sh z.
Пример 18.Выяснить, в каких точках дифференцируема функция 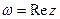 .
.
Дата добавления: 2015-07-14; просмотров: 609;
