Доказательство. По условию функция дифференцируема, следовательно, по определению 25 ее приращение можно записать в виде (9):

По условию функция дифференцируема, следовательно, по определению 25 ее приращение можно записать в виде (9):

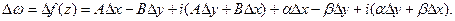
Найдем предел приращения 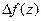в точке z при 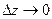, т.е. при :

,

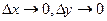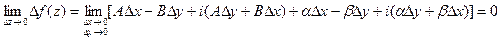По определению 21^/ данное равенство означает, что функция непрерывна в точке z, что и требовалось доказать.

Теорема 4.Для того чтобы функция 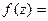u(x,y) + i v(x,y), определенная в некоторой области D, была дифференцируемой в точке z этой области необходимо и достаточно, чтобы в этой области существовали непрерывные частные производные функций u(x,y) и v(x,y) и выполнялись условия

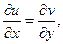
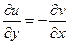, (10)

называемые условиями Коши - Римана или Эйлера – Даламбера, кратко, условиями КРЭДа.