Уравнение Шредингера

Статистическое толкование волн де Бройля и соотношение неопределённостей Гейзенберга привели к выводу, что уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц. Основное уравнение должно быть уравнением относительно волновой функции 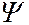. Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э. Шредингером. Оно, как и все основные уравнения физики, не выводится, а постулируется. Его правильность подтверждается тем, что все вытекающие из него следствия согласуются с опытными фактами.

Волновая функция является функцией координат и времени и может быть найдена путем решения уравнения Шредингера. Уравнение Шредингера имеет вид

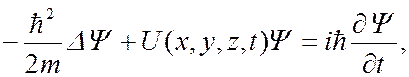(7.44.9)

где 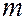– масса частицы; − 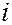мнимая единица; 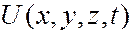– потенциальная функция частицы в силовом поле, в котором она движется; 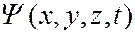– искомая волновая функция; ∆ – оператор Лапласа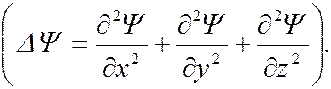

Уравнение (7.44.9) справедливо для любой частицы, движущейся с малой ( 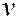<< 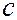) скоростью. Оно дополняется условиями, накладываемыми на волновую функцию: 1) волновая функция должна быть конечной, однозначной и непрерывной; 2) её производные по координатам и времени должны быть непрерывны; 3) функция 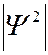должна быть интегрируема. Уравнение (7.44.9) является общим уравнением Шредингера. Его также называют уравнением Шредингера со временем (или временн 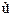м уравнением Шредингера).

Из уравнения (7.44.9) следует, что вид волновой функции 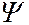определяется потенциальной функцией 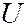(потенциальной энергией), т.е. характером тех сил, которые действуют на частицу. Для многих физических явлений, происходящих в микромире, уравнение (7.44.9) можно упростить, исключив зависимость Ψ от времени, иными словами, найти уравнение Шредингера для стационарных состояний – состояний с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частица движется, стационарно, т.е. функция 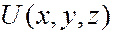не зависит явно от времени и имеет смысл потенциальной энергии. Тогда уравнение Шредингера примет вид

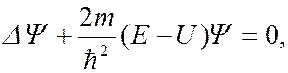(7.44.10)

где 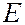– полная энергия частицы. Уравнение (7.44.10) называется уравнением Шредингера для стационарных состояний (или уравнением Шредингера без времени). В этом уравнении функция 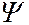должна быть конечной, однозначной и непрерывной во всём рассматриваемом пространстве.

Для электрона в атоме водорода потенциальная энергия равна

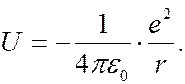(7.44.11)

С учетом этого уравнение Шредингера для электрона в атоме водорода принимает вид:

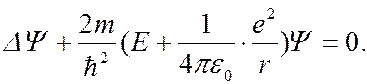(7.44.12)

Для свободной частицы потенциальная энергия 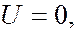поэтому для свободной частицы уравнение Шредингера принимает вид:

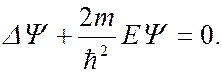(7.44.13)

Малые колебания атомов около положения равновесия в кристаллах и молекулах являются гармоническими. Частица, совершающая гармонические колебания, называется гармоническим осциллятором. Если частица колеблется вдоль направления оси 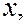потенциальная энергия гармонического осциллятора 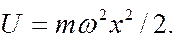Подставив значение потенциальной энергии в выражение (7.44.10), получим уравнение Шредингера для гармонического осциллятора:

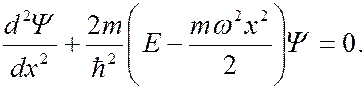(7.44.14)

Значение уравнения Шредингера заключается, например, в том, что оно даёт соответствующее опыту распределение частиц; из него вытекают правила квантования энергии, совпадающие с энергиями стационарных состояний атома водорода в теории Бора. Правила квантования энергии непосредственно вытекают из уравнения Шредингера и условий, налагаемых на волновую функцию (однозначность, конечность, непрерывность). В теории дифференциальных уравнений доказывается, что уравнения такого вида, как уравнение Шредингера, имеют решения, удовлетворяющие вышеприведенным условиям, лишь для некоторых значений энергии. Эти значения энергии, при которых уравнение Шредингера имеет решение, называются собственными значениями энергии. Волновые функции Y, удовлетворяющие уравнению Шредингера (решения уравнения), при данных собственных значениях энергии, называются собственными функциями.