Энергия электрона в атоме водорода

Электрон в атоме водорода движется в кулоновском поле ядра. Его потенциальная энергия равна

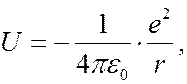
(7.45.1)

где r – расстояние между электроном и ядром. Графически функция изображается на рисунке жирной кривой. с уменьшением (при приближении электрона к ядру) неограниченно убывает.

Уравнение Шредингера имеет в этом случае вид:

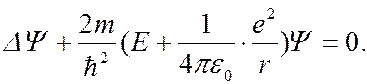(7.45.2)

В теории дифференциальных уравнений доказывается, что уравнения типа (7.45.2) имеют решения, удовлетворяющие однозначности, конечности и непрерывности волновой функции 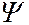, только при отрицательных дискретных собственных значениях энергии

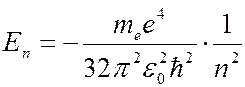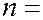( 1, 2, 3, …). (7.45.3)

Таким образом, как и в случае «потенциальной ямы» с бесконечно высокими стенками, решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней. Возможные значения , , 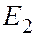,… показаны на рисунке в виде горизонтальных полос. Самый низкий уровень , отвечающий минимальной возможной энергии

– основной, все остальные 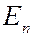( 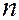= 2, 3, 4,…) – возбужденные. При 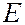< 0 движение электрона является связанным – он находится внутри гиперболической «потенциальной ямы». Из рисунка следует, что по мере роста главного квантового числа 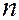энергетические уровни располагаются теснее и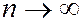 при . При 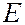> 0 движение электрона становится свободным; область 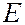> 0 соответствует ионизированному атому.

Итак, если Бору пришлось вводить дополнительные гипотезы (постулаты), то в квантовой механике дискретные значения энергии, являясь следствием самой теории, вытекают непосредственно из решения уравнения Шредингера.