Частица в бесконечно глубокой одномерной потенциальной яме
Рассмотрим поведение частицы в бесконечно глубокой одномерной прямоугольной потенциальной яме.
 Предположим, что частица движется вдоль оси
Предположим, что частица движется вдоль оси 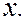 Движение частицы ограничено областью 0 ≤
Движение частицы ограничено областью 0 ≤ 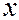 ≤
≤ 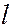 , в которой потенциальная энергия частицы
, в которой потенциальная энергия частицы 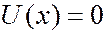 (потенциальная энергия отсчитывается от дна ямы). За пределами ямы при
(потенциальная энергия отсчитывается от дна ямы). За пределами ямы при 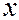 < 0 и
< 0 и 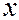 >
> 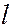 потенциальная энергия
потенциальная энергия 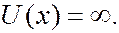 В пределах ямы частица движется свободно. Сталкиваясь со стенками ямы, она отражается от них и изменяет направление своего движения. За пределы потенциальной ямы частица выйти не может. Волновую функцию, зависящую только от одной координаты
В пределах ямы частица движется свободно. Сталкиваясь со стенками ямы, она отражается от них и изменяет направление своего движения. За пределы потенциальной ямы частица выйти не может. Волновую функцию, зависящую только от одной координаты 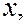 обозначим
обозначим 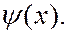 Тогда уравнение Шредингера (7.44.10) примет вид:
Тогда уравнение Шредингера (7.44.10) примет вид:
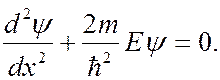 (7.44.15)
(7.44.15)
За пределы ямы частица выйти не может, поэтому вероятность обнаружить ее, а следовательно и волновая функция 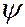 , за пределами ямы равна нулю. Из условия непрерывности следует, что и на границах ямы
, за пределами ямы равна нулю. Из условия непрерывности следует, что и на границах ямы 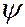 должна быть равна нулю, т.е.:
должна быть равна нулю, т.е.:
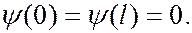 (7.44.16)
(7.44.16)
Этим граничным условиям должны удовлетворять решения уравнения (7.44.15). Обозначим 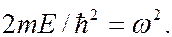 Тогда уравнение (7.44.15) примет вид:
Тогда уравнение (7.44.15) примет вид:
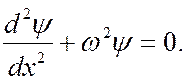 (7.44.17)
(7.44.17)
Решение уравнения (7.44.17) имеет вид:
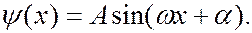 (7.44.18)
(7.44.18)
Значения 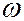 и
и 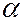 найдем, используя граничные условия (7.44.16). Из условия
найдем, используя граничные условия (7.44.16). Из условия 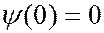 получим:
получим:
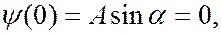
откуда следует, что 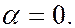 Выполнение условия
Выполнение условия
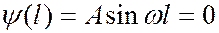
возможно в том случае, если
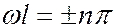
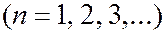 . (7.44.19)
. (7.44.19)
Откуда
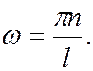 (7.44.20)
(7.44.20)
Из (7.44.19) следует, что решения уравнения будут иметь физический смысл лишь при значениях энергии, удовлетворяющих соотношению:
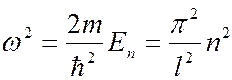 (
( 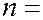 1, 2, 3, …).
1, 2, 3, …).
Отсюда найдем собственные значения энергии:
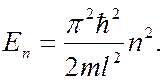 (
( 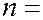 1, 2, 3, … ) (7.44.21)
1, 2, 3, … ) (7.44.21)
Условие квантования энергии получено непосредственно из решения уравнения Шредингера без дополнительных предположений. Подставив (7.44.20) в (7.44.18), получим собственные функции для данной задачи:
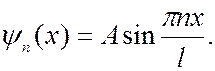 (7.44.22)
(7.44.22)
Коэффициент 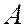 найдем из условия нормирования волновой функции:
найдем из условия нормирования волновой функции:
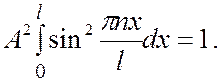 (7.44.23)
(7.44.23)
Откуда
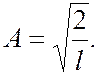 (7.44.24)
(7.44.24)
С учетом (7.44.24) собственные функции принимают вид:
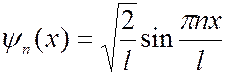 (
( 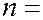 1, 2, 3, …). (7.44.25)
1, 2, 3, …). (7.44.25)
Графики функций 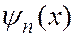
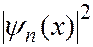 изображены на рисунке для различных значений
изображены на рисунке для различных значений 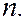
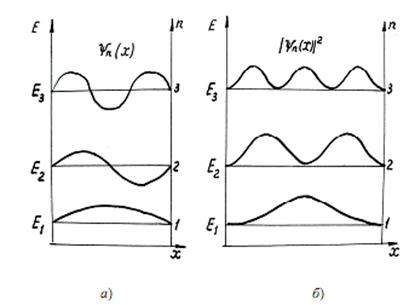
Контрольные вопросы для самоподготовки студентов:
1.Что определяет квадрат модуля волновой функции?
2. Общее уравнение Шредингера.
3.Уравнение Шредингера для стационарных состояний.
Дата добавления: 2015-05-26; просмотров: 2013;
