Соотношение неопределенностей
 Своеобразие волновых свойств частиц прослеживается в следующем эксперименте. Направим на преграду с двумя щелями 1 и 2 параллельный пучок моноэнергетических электронов. За преградой расположим фотопластинку Фп. Сначала закроем щель 2 и пропустим пучок электронов через щель 1. Интенсивность распределения электронов на фотопластинке характеризуется кривой 1. Закроем щель 1 и пропустим пучок электронов через щель 2. Характер распределения электронов в этом случае характеризуется кривой 2. Откроем обе щели. Полученный результат распределения электронов при прохождении через обе щели представлен на кривой в). Эта кривая не является наложением кривых 1 и 2. Она аналогична картине, которая получается при интерференции двух когерентных световых волн. Следовательно, на движение каждого электрона оказывают влияние оба отверстия. Этот вывод несовместим с представлениями о траекториях, по которым движутся электроны. Если бы электрон двигался по определенной траектории, то он проходил бы через определенную щель – первую или вторую. Явление дифракции доказывает, что в прохождении электрона участвуют обе щели.
Своеобразие волновых свойств частиц прослеживается в следующем эксперименте. Направим на преграду с двумя щелями 1 и 2 параллельный пучок моноэнергетических электронов. За преградой расположим фотопластинку Фп. Сначала закроем щель 2 и пропустим пучок электронов через щель 1. Интенсивность распределения электронов на фотопластинке характеризуется кривой 1. Закроем щель 1 и пропустим пучок электронов через щель 2. Характер распределения электронов в этом случае характеризуется кривой 2. Откроем обе щели. Полученный результат распределения электронов при прохождении через обе щели представлен на кривой в). Эта кривая не является наложением кривых 1 и 2. Она аналогична картине, которая получается при интерференции двух когерентных световых волн. Следовательно, на движение каждого электрона оказывают влияние оба отверстия. Этот вывод несовместим с представлениями о траекториях, по которым движутся электроны. Если бы электрон двигался по определенной траектории, то он проходил бы через определенную щель – первую или вторую. Явление дифракции доказывает, что в прохождении электрона участвуют обе щели.
В ряде случаев можно наблюдать, что микрочастицы движутся по определенным траекториям. Например, электрон в камере Вильсона оставляет след, образованный капельками тумана; движение электронов в электроннолучевой трубке рассчитывается по законам классической механики. Следовательно, понятия траектории и определенного местоположения при определенных условиях приближенно применимы к микрочастицам, но только с определенной степенью точности.
Если рассматривать электрон как частицу, то для него характерны следующие свойства:
1. Частица обладает одновременно определенными значениями координаты и импульса.
2. Совокупность последовательных положений движущейся частицы образует определенную линию в пространстве – траекторию.
3. Принцип причинности позволяет определить положение и импульс движущейся частицы на ее траектории в любой последовательный момент времени.
Если электрон волна, то для него все обстоит иначе.
1. Волна протяженна и не сосредоточена в одной точке с определенной координатой.
2. Любая волна характеризуется волновой функцией.
3. Локализация волновой функции может быть различной. Плоская монохроматическая волна (7.43.5) заполняет все бесконечное пространство. Интервал 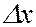 , в котором заключен волновой объект, равен бесконечности. Так как волна монохроматична, то ей отвечает вполне определенный импульс
, в котором заключен волновой объект, равен бесконечности. Так как волна монохроматична, то ей отвечает вполне определенный импульс 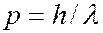 , а интервал, в котором хаключены возможные значения импульса частицы, равен нулю. Если волну локализовать в определенном интервале
, а интервал, в котором хаключены возможные значения импульса частицы, равен нулю. Если волну локализовать в определенном интервале 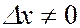 , что можно сделать с помощью волнового пакета - суперпозиции набора волн с длинами от
, что можно сделать с помощью волнового пакета - суперпозиции набора волн с длинами от 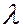 до
до 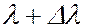 , то при
, то при 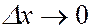 ,
, 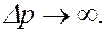 Следовательно, увеличение определенности в локализации волны связано с одновременным возрастанием в неопределенности импульса. Такой волновой пакет имеет вполне определенную координату, но совершенно неопределенный импульс. Волновая природа частиц приводит к тому, что они не могут иметь одновременно определенную координату
Следовательно, увеличение определенности в локализации волны связано с одновременным возрастанием в неопределенности импульса. Такой волновой пакет имеет вполне определенную координату, но совершенно неопределенный импульс. Волновая природа частиц приводит к тому, что они не могут иметь одновременно определенную координату 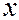 и импульс
и импульс 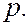
Контрольные вопросы для самоподготовки студентов:
1. Постулаты Бора.
2. В чем заключаются трудности теории Бора?
3. Что называется длиной волны де Бройля?
4. Соотношение неопределенностей Гейзенберга.
Литературные источники:
1. Трофимова, Т.И. Курс физики: учеб. пособие для вузов / Т.И. Трофимова. – М.: ACADEMIA, 2008.
2. Савельев, И.В. Курс общей физики: учеб. пособие для втузов: в 3-х томах / И.В.Савельев. – СПб.: Спец. лит., 2005.
Дата добавления: 2015-05-26; просмотров: 1103;
