Гипотеза де Бройля

Установление корпускулярно-волнового дуализма в оптических явлениях имело очень большое значение для дальнейшего развития физики. Впервые была выявлена двойственная – корпускулярно-волновая – природа физического объекта – электромагнитного излучения. В 1924 г французский физик Луи де Бройль выдвинул смелую гипотезу, согласно которой корпускулярно-волновой дуализм имеет универсальный характер. Согласно гипотезе де Бройля каждая материальная частица обладает волновыми свойствами, причем соотношения, связывающие волновые и корпускулярные характеристики частицы остаются такими же, как и в случае электромагнитного излучения. Напомним, что энергия и импульс фотона связаны с круговой частотой и длиной волны соотношениями

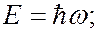
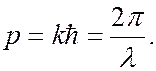(7.43.1)

По гипотезе де Бройля движущейся частице, обладающей энергией 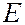и импульсом 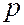, соответствует волновой процесс, частота которого равна

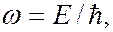(7.43.2)

а длина волны

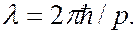(7.43.3)

Как известно, плоская волна с частотой 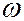, распространяющаяся вдоль оси 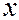, может быть представлена в комплексной форме

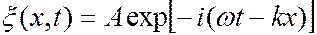(7.43.4)

где 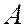– амплитуда волны, а 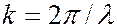– волновое число.

Согласно гипотезе де Бройля свободной частице с энергией 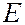и импульсом 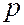, движущейся вдоль оси 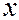, соответствует плоская волна

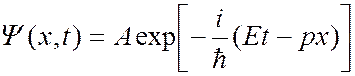, (7.43.5)

распространяющаяся в том же направлении и описывающая волновые свойства частицы. Эту волну называют волной де Бройля. Соотношения, связывающие волновые и корпускулярные свойства частицы

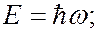
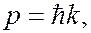(7.43.6)

где 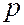импульс частицы, а 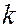- волновой вектор, получили название уравнений де Бройля.

Свойства волн де Бройля. Рассмотрим свойства, которыми обладают волны де Бройля. Прежде всего, следует отметить, что волны материи – волны де Бройля – в процессе распространения могут отражаться, преломляться, интерферировать и дифрагировать по обычным волновым законам. Найдем фазовую скорость волн де Бройля 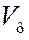, т.е. скорость, с которой распространяются точки волны с постоянной фазой. Пусть частица движется вдоль оси 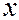, тогда условие постоянства фазы волны (7.43.5) имеет вид

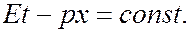
Дифференцируя это соотношение, находим

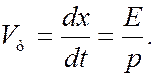
Поскольку 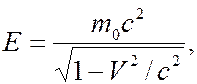а

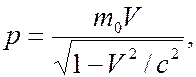
где 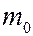– масса покоя частицы, а – 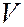ее скорость, то для фазовой скорости волны де Бройля получаем следующее выражение

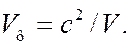(7.43.7)

Так как 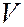< 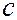, то фазовая скорость волны де Бройля 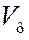оказывается больше скорости света в вакууме 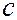. Это не противоречит теории относительности, которая запрещает движение со скоростью, большей скорости света. Ограничения, накладываемые теорией относительности, справедливы лишь для процессов, связанных с переносом массы или энергии. Фазовая скорость волны не характеризует ни один из этих процессов, поэтому на ее величину не накладывается никаких ограничений.

Найдем теперь групповую скорость 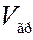волны де Бройля. По определению

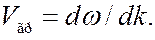(7.43.8)

Преобразуем это выражение:

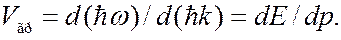(7.43.9)

Энергия 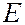и импульс 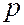в теории относительности связаны между собой соотношением:

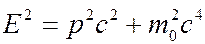. (7.43.10)

Дифференцируя это выражение, находим

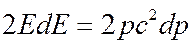
или

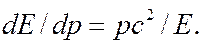
Отсюда

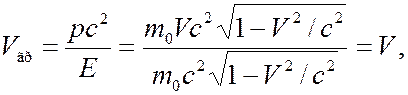(7.43.11)

т.е. групповая скорость 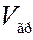волны де Бройля равна скорости движения частицы .

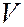В случае нерелятивистской частицы, скорость которой 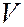<< 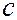, длина волны де Бройля равна

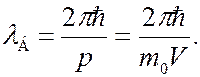(7.43.12)

Если известна кинетическая энергия 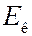нерелятивистской частицы, то для длины волны де Бройля получаем выражение

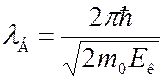. (7.43.13)

В релятивистском случае, когда скорость частицы 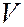сравнима со скоростью света в вакууме 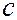, длина волны де Бройля равна

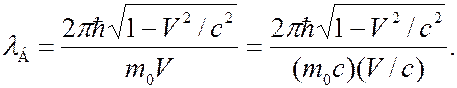(7.43.14)

Для релятивистской частицы связь между импульсом 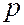и полной энергией частицы 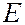определяется соотношением (7.43.10), длина волны де Бройля в этом случае равна

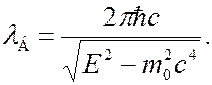(7.43.15)

Полная энергия 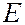и кинетическая энергия 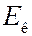релятивистской частицы связаны между собой соотношением:

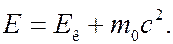(7.43.16)

Подставив (7.43.16) в (7.43.15), выразим длину волны де Бройля релятивисткой частицы через ее кинетическую энергию:

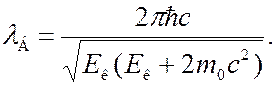(7.43.17)

Найдем длину волны де Бройля электрона, прошедшего ускоряющую разность потенциалов 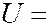150,4 В. В этом случае электрон будет нереятивистским. По формуле (7.43.13) получим:

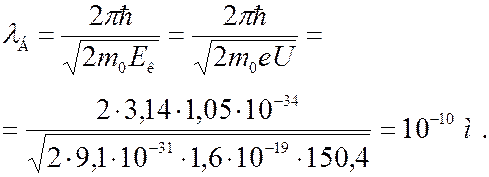
Таким образом, при значении ускоряющей разности потенциалов в пределах от десятков вольт до нескольких киловольт де бройлевская длина волны электрона по порядку величины будет составлять 10^{-10 м, что сравнимо с величиной периода кристаллической решетки.}

Найдем теперь длину волны де Бройля для макроскопического, но достаточно малого объекта – пылинки, масса которой 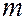= 1 г, а скорость 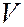= 1см/c . Используя соотношение (12), получае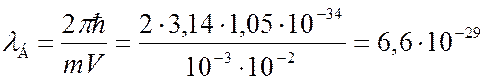м:

м.

Найденная длина волны значительно меньше не только размеров самой пылинки, но и наименьшего известного в физике размера – радиуса ядра, составляющего по порядку величины 10^{-15 м. Такую длину волны экспериментально нельзя измерить.}

Таким образом, волновые свойства частиц будут наиболее ярко проявляться в тех случаях, когда дебройлевская длина волны 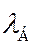частицы сравнима с характерными размерами области движения частицы 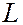, т.е. 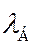~ 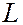. В первом из разобранных выше примеров примеров дебройлевская длина волны электрона , размеры атома и расстояние между атомами в кристалле имеют один и тот же порядок величины. Это означает, что при взаимодействии электронов с атомами, а также при их движении в твердых телах волновые свойства электронов будут проявляться максимальным образом. В тех же случаях, когда 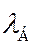<< 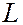, как, например, для рассмотренной выше пылинки, волновые свойства частицы становятся несущественными, и для описания движения таких объектов необходимо пользоваться законами классической механики.