Экспериментальные подтверждения гипотезы де Бройля

Критерием истинности любой физической теории, любой гипотезы всегда является эксперимент. Первые экспериментальные исследования, подтвердившие волновую природу частиц, были выполнены американскими физиками К. Дэвиссоном и Л. Джермером, а также независимо английским физиком Дж. П. Томсоном в 1927г. В этих работах использовалась дифракция электронов на кристаллической решетке. Как уже обсуждалось выше, дебройлевская длина волны электрона при не очень большом значении ускоряющей разности потенциалов (~100 В) по порядку величины составляет 10 ^-10 м. Этот же порядок величины характерен для расстояния между атомными плоскостями в кристалле. Поэтому, так же, как и в случае рентгеновских лучей, кристалл может играть роль дифракционной решетки для электронных волн.

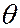Рассмотрим дифракцию электронов на совершенном кристалле, т.е. кристалле, обладающем идеальной, без каких-либо нарушений кристаллической решеткой. Пусть электроны падают на кристалл под углом скольжения по отношению к рассеивающему семейству плоскостей. Для простоты рассмотрим симметричный случай, когда поверхность кристалла параллельна рассеивающим плоскостям (см. рисунок). Тогда угол 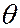будет углом скольжения, под которым электроны падают на поверхность кристалла, а угол 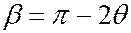– углом между падающим и дифрагировавшим пучками электронов.

Теоретический анализ дифракции электронов на кристаллах во многом аналогичен случаю рентгеновских лучей. При значении угла 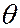, удовлетворяющем условию Брэгга-Вульфа

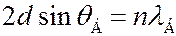(7.43.18)

возникает интенсивный дифракционный максимум отраженной волны. Здесь 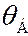– брэгговский угол, 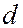– расстояние между отражающими плоскостями (постоянная решетки кристалла), 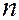– целое число, принимающее значения 1, 2, 3, ... , называемое порядком отражения.

Физический смысл условия Брэгга-Вульфа (7.43.18) достаточно прозрачен: дифракционный максимум появляется в тех случаях, когда разность хода волн, отраженных от соседних атомных плоскостей, равна целому числу длин волн де Бройля. Именно в этом случае отраженные волны усиливают друг друга, т.е. имеет место конструктивная интерференция.

Опыт Дэвиссона и Джермера. Дэвиссон и Джермер исследовали дифракцию электронов на монокристалле никеля, кристаллическая структура которого была известна из опытов по дифракции рентгеновских лучей. Схема их эксперимента представлена на рисунке.

Электроны от электронной пушки 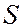, прошедшие ускоряющую разность потенциалов 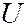, падали нормально на сошлифованную поверхность кристалла никеля 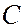. С помощью детектора 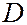исследовалось число электронов, отраженных от кристалла под углом при различных значениях. Кристаллическая решетка в опыте Дэвиссона и Джермера играла роль объемной отражательной дифракционной решетки. В опытах Дэвиссона и Джермера дифракционный максимум под углом 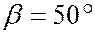(максимальное отражение электронов) наблюдался при ускоряющей разности потенциалов 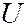= 54 В, что соответствует дебройлевской длине волны

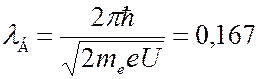нм.

Длина волны, определяемая из условия Брэгга-Вульфа (7.43.18) для постоянной решетки никеля 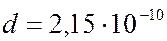м равнялась 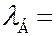0,165 нм. Это совпадение экспериментальных и расчетных значений служит прекрасным подтверждением гипотезы де Бройля о наличии у частиц волновых свойств.

Опыт Дж. П. Томсона. В экспериментах Томсона исследовалась дифракция электронов на поликристаллическом образце. Коллимированный пучок моноэнергетических электронов падал нормально на тонкую металлическую поликристаллическую фольгу. На фотопластинке, расположенной за фольгой, прошедшие электроны образовывали дифракционную картину в виде тонких концентрических колец. Поликристалл состоит из большого числа очень маленьких монокристаллических зерен - кристаллитов, которые хаотически ориентированы по отношению друг к другу. При падении пучка электронов на поликристалл в нем всегда найдутся кристаллиты, ориентированные так, что для какой-либо система атомных плоскостей будет будет выполняться условие Брэгга-Вульфа (7.43.18)

.

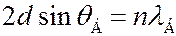Ввиду осевой симметрии, вклад в дифракционное отражение будут также давать кристаллиты, у которых рассматриваемые отражающие плоскости повернуты относительно оси, задаваемой направлением падения электронов, при условии, что падение осуществляется под тем же углом 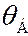. Следовательно, в случае поликристалла дифракционное отражение от одного семейства плоскостей при фиксированном значении будет происходить в конус с углом раствора 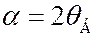. Сечение этого конуса плоскостью фотопластинки дает окружность. Вклад в отражение от разных плоскостей кристалла (разные значения 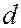), а также учет различных порядков отражения приводит к появлению на фотопластинке системы концентрических окружностей.

Дифракция одиночных электронов. Рассмотренные выше эксперименты проводились с достаточно интенсивными пучками частиц, в данном случае электронов. Поэтому выявленные в них волновые свойства могли быть приписаны как ансамблю взаимодействующих между собою электронов, так и отдельному электрону. Для того, чтобы выяснить, обладает ли индивидуальная частица волновыми свойствами, группа отечественных физиков во главе с В.А. Фабрикантом выполнила в 1949 г дифракционные исследования с очень слабым пучком электронов.

В этих опытах промежуток времени между двумя последовательными прохождениями электронов через кристалл в 30000 раз превышал время, затрачиваемое одним электроном на прохождение всего прибора. Таким образом, электроны дифрагировали в кристалле поодиночке и полностью исключалось взаимодействие электронов друг с другом как причина возникновения дифракционной картины. При достаточной длительности эксперимента распределение точек приобретает характерный для дифракции на поликристалле вид концентрических колец (см. рисунок). Таким образом было доказано, что волновые свойства присущи отдельному электрону.

Дифракционные опыты с тяжелыми частицами - атомами, молекулами, нейтронами - показали, что гипотеза де Бройля имеет универсальное значение. Все частицы, независимо от их природы и внутреннего строения обладают волновыми свойствами.