Квантовые числа

В квантовой механике доказывается, что уравнению Шредингера удовлетворяют собственные функции 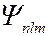, определяемые набором трёх целочисленных параметров – квантовых чисел: главного 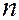, орбитального 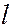и магнитного .

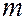Главное квантовое число 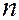характеризует расстояние электрона от ядра – радиус орбиты, определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения, начиная с единицы ( 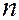= 1, 2, 3,…). В атомной физике состояния электрона, соответствующие главному квантовому числу 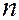, ( 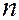= 1, 2, 3, 4,…) принято обозначать буквами

Орбитальное (азимутальное) квантовое число 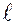определяет величину орбитального момента количества движения (момента импульса) 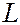электрона в сферически-симметричном поле:

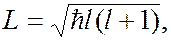(7.45.4)

а также форму распределения амплитуды волновой функции электрона в атоме, т.е. форму электронного облака (форму атомной орбитали). Определяет подуровень энергетического уровня, задаваемого главным квантовым числом 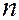,и при данном 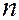может принимать значения 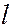= 0, 1, 2, … 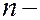1. Область пространства, в которой высока вероятность обнаружить электрон (не менее 0,95), называют орбиталью. Согласно квантовой механике, не существует определенных круговых орбит электронов, как в теории Бора. В силу волновой природы электрон «размазан» в пространстве, подобно «облаку» отрицательного заряда. 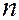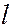Квантовые числа и определяют размер и форму электронного облака, магнитное число 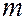– ориентацию облака в пространстве. Основные типы орбиталей обозначают буквами 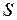, , 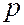, , 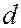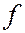…(от слов sharp, principal, diffuse, fundamental).Состояние электрона,

характеризующееся квантовыми числами 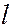= 0 называют 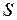-состоянием, 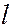= 1 – 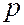-состоянием, 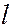=2 – 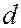-состоянием, 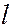= 3 – 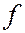-состоянием и т.д. Значение главного квантового числа указывается перед обозначением орбитального квантового числа Возможны следующие состояния электрона (орбитали):

и т.д.

Вид двух основных типов орбиталей 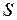(она одна), 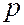(их три), по которым «размазан» электронный заряд, показан на рисунке.

Орбитали часто называют оболочками слоев, поскольку они характеризуют формы разных орбит, на которых можно обнаружить электроны, находящиеся в одном слое (при заданном квантовом числе ).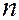

Магнитное квантовое число 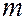– квантовое число, определяющее величину проекции 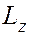момента количества движения (момента импульса) электрона на заданное направление (ось – направление магнитного поля):

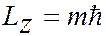. (7.5.5)

Магнитное квантовое число принимает 2 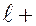1 целых значений (от 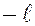до ), где 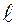– орбитальное (азимутальное) квантовое число. На рисунке показаны прекции момента имульса 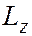при различных значениях 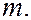Соотношения (7.5.4) и (7.5.5) показывают, что момент количества движения электрона и проекция этого момента являются также квантованными величинами.

Каждому 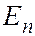(кроме ) соответствует несколько волновых функций 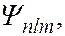отличающихся значениями квантовых чисел 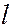и 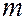. Это означает, что атом водорода может иметь одно и то же значение энергии, находясь в различных состояниях. Состояния с одинаковой энергией называются вырожденными, а число вырожденных состояний с одинаковым значением энергии называется кратностью вырождения. Каждое значение энергии 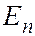имеет кратность вырождения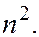

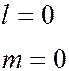
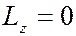
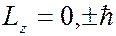
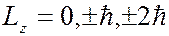
Наличие магнитного квантового числа 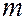приводит в магнитном поле к расщеплению уровня с главным квантовым числом 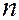на 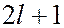подуровней, что должно привести к расщеплению спектральных линий. Расщепление энергетических уровней в магнитном поле назывется эффектом Зеемана.

Расщепление энергетических уровней в электрическом поле назывется эффектом Штарка.

На рисунке представлена схема энергетических уровней атома водорода с учетом вырождения, на которой показаны переходы, приводящие к возникновению серий Лаймана, Бальмера, Пашена, Брекета. В квантовой механике доказывется, что возможны только такие переходы, при которых квантовое число 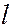меняется на единицу:

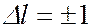(7.5.6.).

Условие (7.5.6) называется правилом отбора, которое является следствием закона сохранения момента количества движения. С учетом правила отбора серии Лаймана соответствуют следующие переходы электронов в атоме водорода: np→1s (n = 2, 3, …); серии Бальмера – переходы электронов: np→2s, ns→ 2p, nd→ 2p (n =3, 4, 5, …); серии Пашена – переходы 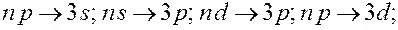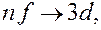где 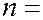4. 5, 6, …

Как уже говорилось выше, электрон размазан вокруг ядра в виде электронного облака. Собственные функции определяют распределение в пространстве плотности вероятности

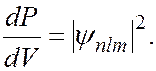
На рисунке приведены распределения плотности вероятности для различных значений квантовых чисел и (За единицу измерения принят радиус первой боровской орбиты). Вероятность найти электрон отлична от нуля при любых значениях , но максимальна при значениях радиуса, совпадающего с радиусами орбит, определенных по теории Бора (7.42.16).