F и Τ числа

Кроме ФПМ и ЧКХ есть и другая важная характеристика объективов: F‑число (F‑number, F‑stop). F‑число характеризует яркость сформированного линзой изображения. Оно обычно нанесено на объективе в виде F/1.4 или иногда в другой форме 1:1.4 (Величина, обратная числу F, называется относительным отверстием, то есть, например, если F=1.4, то относительное отверстие 1:1.4. Однако на практике нередко относительным отверстием называют само число F, то есть в нашем примере, 1.4. Прим. ред .). F‑число зависит от фокусного расстояния объектива и эффективного диаметра области, через которую проходят лучи света. Эта область может изменяться передвижением механических лепестков, которые мы обычно называем ирисовой диафрагмой.

Следует отметить, что эффективный диаметр объектива – это отнюдь не действительный диаметр объектива, а диаметр изображения диафрагмы, если смотреть на него с передней стороны объектива.

Первый диаметр обычно называется входным зрачком. А есть еще и выходной зрачок, как показано на рис. 3.21. Сама ирисовая диафрагма расположена между этими двумя зрачками и между двумя главными точками.

Чем меньше F‑число, тем больше отверстие диафрагмы и тем больше света проходит через объектив. Минимальное F‑число для данного объектива нанесено на самом объективе и характеризует способность объектива собирать свет.

Часто объективы с низким F‑числом (F‑stop) называются светосильными объективами или быстрыми объективами (faster lens ). Это потому, что на заре фотографии пытались сократить время экспозиции пленки путем увеличения количества света (низкое F‑число); это позволяло сделать снимок быстро и получить картинку без потери четкости, вызванной дрожанием камеры.

Допустим, 16 мм‑объектив имеет минимальное F‑число, равное 1.4, тогда это записывается так: 16 мм/1.4 или 16 мм 1:1.4. Максимальное эффективное отверстие диафрагмы эквивалентно кругу с диаметром 16/1.4 = 11.43 мм – эквивалентно потому, что лепестки диафрагмы образуют треугольное, квадратное, пятиугольное или шестиугольное отверстие.

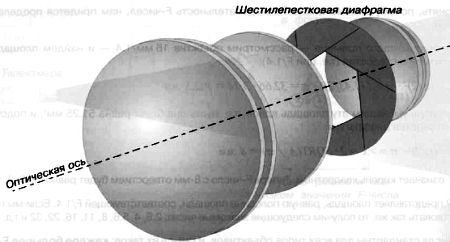
Рис. 3.20. Положение и размер диафрагмы зависят от типа и конструкции объектива

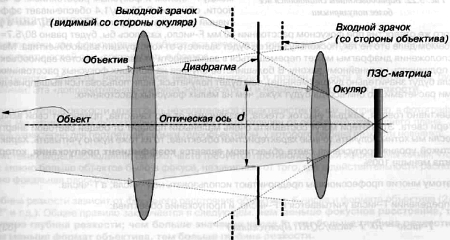
Рис. 3.21. Определение положения диафрагмы

Чтобы понять, почему именно такова последовательность F‑чисел, нам придется проделать ряд вычислений.

Начнем с предыдущего примера – рассмотрим объектив 16 мм/1.4 – и найдем площадь полностью открытого отверстия (т. е. при F/1.4):

A_1.4 = (d/2)²∙π = (11.43/2)²∙π = 32.66∙3.14 = 102.5 мм² (31)

Давайте теперь уменьшим эту площадь вдвое, т. е. пусть она будет равна 51.25 мм², и подсчитаем диаметр отверстия диафрагмы:

A_х = (х/2)²∙π => х = 2∙SQRT(A_х/π) = 8 мм (32)

Где SQRT означает корень квадратный. Теперь F‑число с 8‑мм отверстием будет равно 16/8 = 2, т. е. F/2.

Здесь F/2 представляет площадь, равную половине площади, соответствующей F/1.4. Если мы продолжим действовать так же, то получим следующие знакомые числа: 2.8, 4, 5.6, 8, 11, 16, 22, 32 и т. д.

Все эти числа стандартны для всех типов объективов, и смысл их таков: каждое большее F‑число пропускает половину светового потока по сравнению с предыдущим F‑числом.

Теперь становится намного понятнее, почему телекамера с объективом 16 мм/1.0 более чувствительна, чем та же телекамера с объективом 16 мм/1.4.

Для вариообъективов приведенные здесь F‑числа относятся к отверстию диафрагмы на минимальном фокусном расстоянии вариообъектива. Очевидно, что при этом получается наилучшее «светособирающее число» для любого объектива. Для вариообъектива при установке наибольшего фокусного расстояния F‑число всегда меньше, чем на минимальном фокусном расстоянии. Но было бы ошибкой предполагать линейную зависимость между F‑числом и фокусным расстоянием. В частности, объектив 8‑80 мм/1.4 обеспечивает эффектакого же отверстия при фокусном расстоянии 80 мм F‑число, казалось бы, будет равно 80/5.7 = 14.

На самом деле это не так, поскольку многое будет зависеть от конструкции вариообъектива. Место расположения диафрагмы может перемещаться в зависимости от движения частей вариообъектива, подчиняясь нелинейному закону. В большинстве случаев на больших фокусных расстояниях F‑числа будут значительно лучше (меньше), чем будет получаться, если пользоваться вышеприведенными расчетами, но они всегда будут хуже, чем на малых фокусных расстояниях.

Объективно говоря, каждый участок стекла, независимо от его качества, привносит свой вклад в потери света. Эти потери могут составлять очень маленький процент от общей световой энергии, но если мы хотим получить точные характеристики объектива, то их тоже нужно учитывать. Характеристикой уровня пропускания света объективом является коэффициент пропускания, который всегда меньше 100 %.

Поэтому многие профессионалы предпочитают использовать не F‑числа, аТ‑числа. В определении Т‑числа учитывается и F‑число, и пропускание объектива:

Т‑число = 10·F‑число/SQRT(Пропускание) (33)

Поскольку пропускание объектива, как уже упоминалось, всегда меньше 100 % (обычно от 95 % до 99 %), то очевидно, что Т‑число будет несколько больше, чем F‑число.

Рис. 3.22. Вариообъективы становятся все более популярными