S-Состояние электрона в атоме водорода

1s-Состояние электрона в атоме водорода является сферически-симметричным, т. е. не зависит от углов qи j. Волновая функция ф электрона в этом состоянии определяется только расстоянием r электрона от ядра, т. е.

Y = Y₁₀₀(r), где цифры в индексе соответственно указывают, что n = 1, l = 0и m_l = 0. Уравнению Шредингера для 1s-состояния электрона в атоме водорода удовлетворяет функция вида

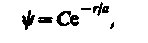(224.1)

где, как можно показать, а = h²4pe₀/(me²)- величина, совпадающая с первым боровским радиусом а (см. (212.2)) для атома водорода, С - некоторая постоянная, определяемая из условия нормировки вероятностей (216.3).

Благодаря сферической симметрии Y-функции вероятность обнаружения электрона на расстоянии rодинакова по всем направлениям. Поэтому элемент объема dV,отвечающий одинаковой плотности вероятности, обычно представляют в виде объема сферического слоя радиусом rи толщиной dr. dV = 4pr²dr. Тогда, согласно условию нормировки вероятностей (216.3) с учетом (224.1),

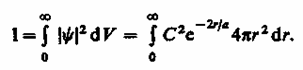
После интегрирования получим

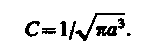(224.2)

Подставив выражение (224.2) в формулу (224.1), определим нормированную волновую функцию, отвечающую 1s-состоянию электрона в атоме водорода:

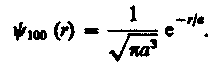(224.3)

Вероятность обнаружить электрон в элементе объема (см. (216.2)) равна

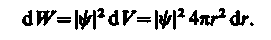
Подставив в эту формулу волновую функцию (224.3), получим

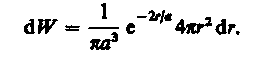
Вычислим те расстояния r_maxот ядра, на которых электрон может быть обнаружен с наибольшей вероятностью. Исследуя выражение dW/drна максимум, получим, что r_max = а. Следовательно, электрон может быть обнаружен с наибольшей вероятностью на расстояниях, равных боровскому радиусу, т. е. имеется равная и наибольшая вероятность обнаружения электрона во всех точках, расположенных на сферах радиуса а с центром в ядре атома. Казалось бы, квантово-механический расчет дает полное согласие с теорией Бора. Однако, согласно квантовой механике, плотность вероятности лишь при r = а достигает максимума, оставаясь отличной от нуля во всем пространстве (рис. 305).

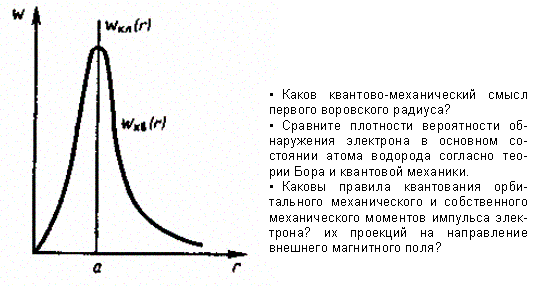
Рис. 305

Таким образом, в основном состоянии атома водорода наиболее вероятным расстоянием от электрона до ядра является расстояние, равное боровскому радиусу. В этом заключается квантово-механический смысл воровского радиуса.