Фільтр Кауера.

Фільтри Баттерворта і Чебишева мають передатні функції, що за формою являють собою постійну, ділену на поліном. Це означає, що всі нулі передачі розташовуються в s = ∞. У деяких випадках це не буде ідеальним рішенням. Кауер показав, що можна одержати набагато кращу апроксимацію ідеалізованих амплітудно-частотних характеристик фільтрів нижніх частот, якщо використовувати фільтр із кінцевими нулями передачі. Він знайшов, що при належному виборі нулів і полюсів можна спроектувати фільтр із равнохвильовим загасанням як у смузі прозорості, так і в смузі затримування. Оскільки координати нулів у таких фільтрах визначаються еліптичними функціями класичної теорії поля, ці фільтри часто називають еліптичними.

При цій апроксимації загасання в смузі прозорості коливається між нулем і заданим максимумом 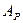, як і при Чебишевській апроксимації, а загасання в смузі затримування коливається між нескінченністю і заданим мінімумом .

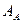Еліптична апроксимація більш ефективна, ніж дві попередні, у тому сенсі, що вона забезпечує більш крутий перехід від смуги прозорості до смуги затримування при заданому порядку апроксимації.

Для еліптичної апроксимації загасання задається формулою:

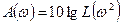, (8.11)

де ;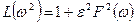

.

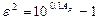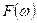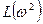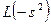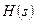Функція й у свою чергу , і в цьому випадку є відношенням поліномів:

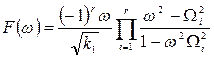, (8.12)

де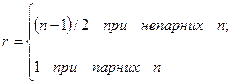

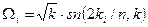при .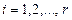

Наступний етап полягає у визначенні нулів і полюсів. Нулі 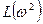можуть бути знайдені за допомогою співвідношення 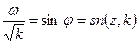. У свою чергу нулі 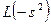можна одержати за допомогою підстановк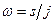и . При 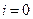мається дійсний нуль 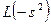у точці 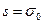, де

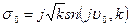. (8.13)

А при 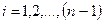мається 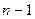різних комплексних нулів у точках:

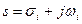, (8.14)

де .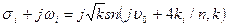

Нулі, що залишилися, відрізняються від уже знайдених коефіцієнтом (-1), отже (8.14) можна переписати у виді:

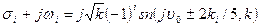, (8.15)

при .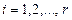

За допомогою формули додавання еліптичних функцій можна показати, що:

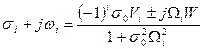, при 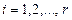(8.16)

де ;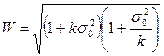

;

.

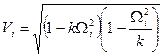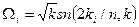Тепер мається повний опис функції 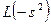. Вона має нулі в точках 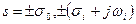і дворазові полюси в крапках 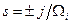, які можна знайти, використовуючи розкладання еліптичних функцій у ряд, використовуючи це розкладання можна записати у виді:

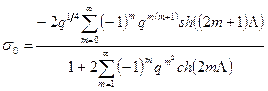, (8.17)

де .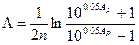

Параметр q, називаний модулярною постійною, задається вираженням:

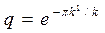. (8.18)

Аналогічно з (8.16) одержуємо:

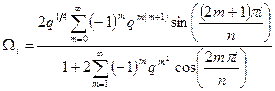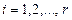, . (8.19)

Ряди в (8.17) і (8.19) швидко сходяться і тому в більшості випадків досить трьох або чотирьох членів ряду.

Модулярну постійну q можна визначити таким чином.

Тому що 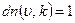те 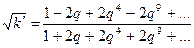. (8.20)

Оскільки 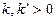, те 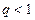і, отже, першим наближенням для q є 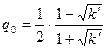. Заміняючи 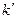на (8.20) і зробивши розподіл одержуємо:

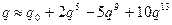. (8.21)

Таким чином, якщо 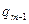- деяке наближення для q, те 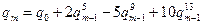є кращим наближенням, ніж 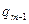. Використовуючи повторно це рекурентне співвідношення, можна показати, що:

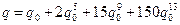. (8.22)

Тому що 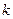відомо, те можна оцінит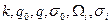и й 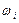і потім сформувати нормовану передатну функцію .

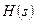Для заданого порядку 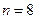, , 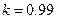і 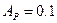дБ результуюче мінімальне загасання в смузі затримування задається формулою:

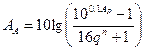, (8.23)

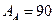дБ.

За формулами (8.16), (8.17), (8.19) обчислюємо координати нулів і полюсів (рис. 8.8, 8.9), координати яких приведені в таблиці 8.3.

Як видно з графіка полюси еліптичного фільтра знаходяться поблизу уявної осі s-площини, що свідчить про те, що фільтр знаходиться на межі стійкості, тобто він дуже чутливий до зміни параметрів передатної функції. Це накладає додаткові вимоги до точності параметрів при реалізації даного фільтра, а також при перебуванні необхідної передатної функції. Виходячи з цього, при розрахунках необхідно обчислювати з точністю не менш восьми знаків після коми.

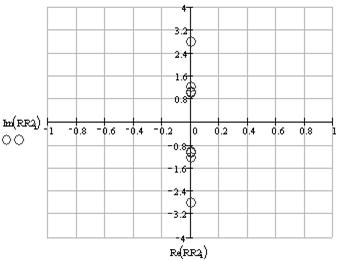
Рис. 8.8. – Розташування нулів на комплексній s-площині.

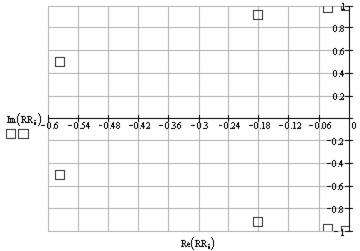
Рис. 8.9. – Розташування полюсів на комплексній s-площині.

Таблиця 8.3. – Координати полюсів і нулів на комплексній площині

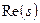
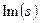
Нулі		±2,7942373
	±1,2366291
	±1,0489877
	±1,0130226
Полюси	-0,57862	±0,5041528
-0,18407	±0,9138925
-0,04334	±0,9817762
-0,07702	±0,9956549

Розрахуємо необхідні коефіцієнти для передатної функції.

Нормована передатна функція еліптичного фільтра нижніх частот з коефіцієнтом вибірковості k, максимальним загасанням у смузі прозорості A_p дБ, мінімальним загасанням у смузі затримування, рівним чи великої A_A дБ, має передатну функцію:

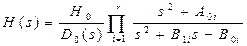, (8.24)

де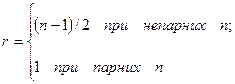

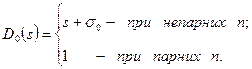
Коефіцієнти передатної функції і постійна 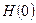обчислюються в такий спосіб відповідно до виражень (8.12)-(8.23).

, ;

, ;

, ;

, ;

, ;

, ;

,

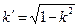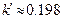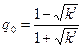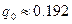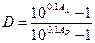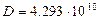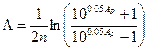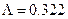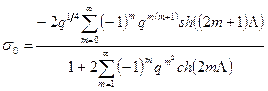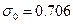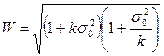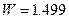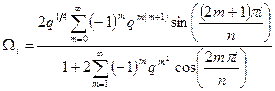Таблиця 8.4

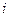
Wi	0.35787941129755	0.808649867719332	0.953299992370837	0.987144797922262

,

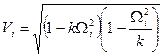Таблиця 8.5

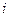
Vi	0.871892945306218	0.345707255006063	0.08920414776143	0.0162090610494

,

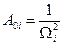Таблиця 8.6

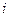
A0i	8.80776208949712	1.52925165901754	1.10037526868088	1.02621480911187

,

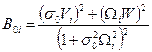Таблиця 8.7

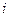
B0i	0.588919259676379	0.86908603318616	0.968511334859571	0.991376153404562

,

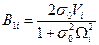Таблиця 8.8

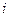
B1i	1.15723802668585	0.368147121881639	0.08668892152741	0.015404962994466

Величини 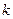і 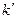рівні відповідно:

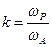- коефіцієнт вибірковості, ;

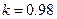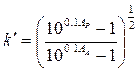- коефіцієнт дискримінації, .

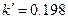Після підстановки отриманих значень коефіцієнтів у (8.24) ми одержимо:

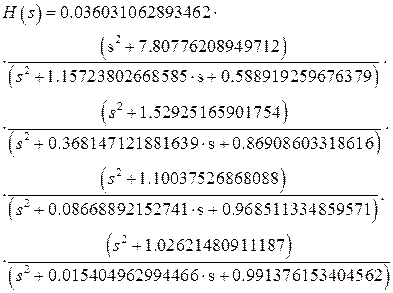(8.25)

Після спрощення одержимо вираження для аналогового еліптичного фільтра нижніх частот:

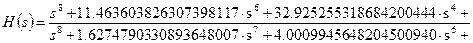
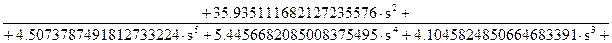
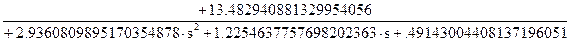(8.26)

Амплітудно-частотна характеристика нормованого еліптичного фільтра нижніх частот приведена на рис. 8.10.

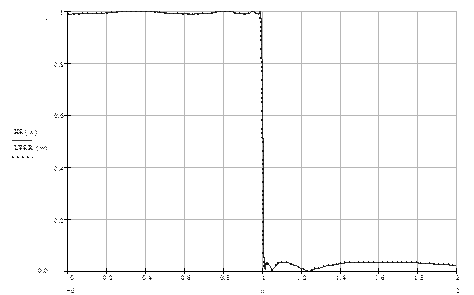
Рис. 8.10. – Амплітудно-частотна характеристика нормованого еліптичного фільтра, n=8.

Для порівняння отриманих передатних характеристик нормованих фільтрів нижніх частот розглянемо іншу складову частину частотної характеристики фільтра – фазочастотну характеристику (фазовий кут) 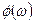, і характеристику групового часу 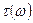, що визначаються вираженнями:

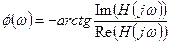, (8.27)

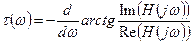. (8.28)

Фільтри, включені в обробку сигналів повинні володіти найбільш лінійною фазочастотною характеристикою, що еквівалентно груповому часові, по можливості, близькому до постійної величини. Невеликі відхилення фазочастотної характеристики від лінійної будуть вносити різноманітні перекручування в імпульсну характеристику і, отже, призведуть до помилок в оцінці часу проходження сигналів.

Фазові характеристики фільтрів Баттерворта, Чебишева, та еліптичного 8-го порядку наведені на рисунках 8.11–8.13.

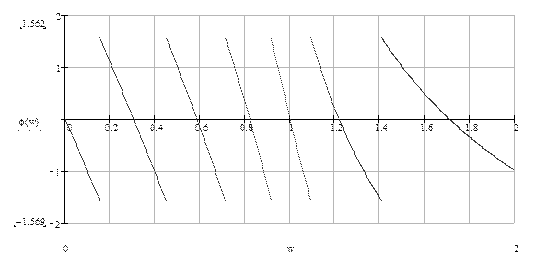
Рис. 8.11 – Фазо-частотна характеристика

Фільтра Баттерворта 8-го порядку.

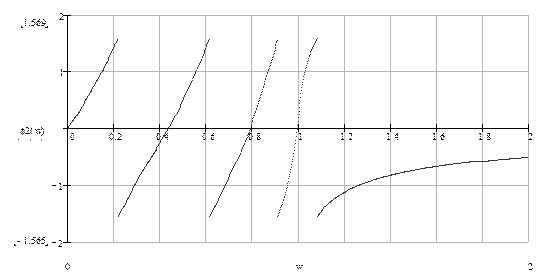
Рис. 8.12 – Фазова характеристика фільтра Чебишева 8-го порядку.

Видно, що у всіх типів фільтрів фазова характеристика сильно перекручена, особливо поблизу частоти зрізу 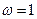, що обумовлено деформацією частотної шкали, а також фазовою нелінійністю апроксимацій.

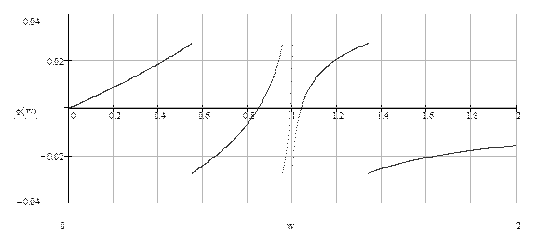
Рис. 8.13. – Фазова характеристика еліптичного фільтра 8-го порядку.

Фазова нелінійність виявляється сильніше при збільшенні порядку фільтра, і зменшується при зменшенні порядку. Однак важко забезпечити одночасно і постійну групову затримку, і задану характеристику фільтра.

На рисунках 8.14-8.15 приведені характеристики групової затримки сигналів.

Рис. 8.14 – Груповий час затримки для фільтрів Баттерворта ( 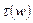) і Чебишева ( 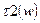) 8-го порядку.

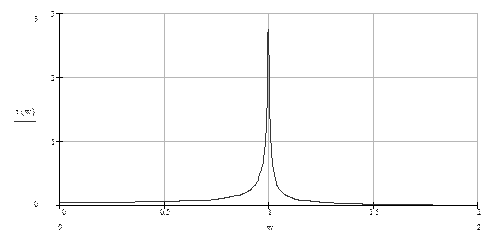
Рис. 8.15 – Груповий час затримки

еліптичного фільтра 8-го порядку.

Варто звернути увагу на те, що найменшу нелінійність фазової характеристики має фільтр Баттерворта, але еліптичний фільтр більш вигідний, тому що для тих самих вимог до АЧХ, він буде мати порядок набагато нижче з кращою фазовою характеристикою. У фільтрів Баттерворта і Чебишева принципово неприпустиме зрушення фази на –2700, що спостерігається при астатизмі 3-го порядку, тому що система буде не стійкою. Еліптична апроксимація дозволяє за рахунок нулів полінома чисельника зменшити фазові зрушення. Тому для числа нулів 8 зрушення +180 ми одержимо –270+180 = –90. На підставі цього, для подальшого розрахунку фільтра варто використовувати передатну функцію еліптичного фільтра.

Вибір фільтру відбувається так, як правило, спочатку задаються необхідна рівномірність характеристики в смузі пропускання і необхідне загасання на деякій частоті зовні смуги пропускання і деякі інші параметри. Після цього вибирається сама відповідна схема з кількістю полюсів, достатньою для того, щоб задовольнялися всі ці вимоги. Є три найпопулярніших схеми фільтрів, а саме фільтр Баттерворта (максимально плоска характеристика в смузі пропускання), фільтр Чебишева (найкрутіший перехід від смуги пропускання до смуги придушення) і фільтр Бесселя (максимально плоска характеристика часу запізнювання). Будь-якій з цих типів фільтрів можна реалізувати за допомогою різних схем фільтрів. Всі вони різним чином годяться для побудови фільтрів верхніх і нижніх частот, а так само смугових фільтрів. Передавальні функції цифрового фільтру будь-якого типу конструюються на основі передавальних функцій аналогових фільтрів-прототипів за допомогою білінійного z-перетворення частоти.

Контрольні запитання

1. Що необхідно для розрахунку аналогових фільтрів?

2. Навести основні типи фільтрів.

3. Обґрунтувати етапи побудови фільтру.

4. Узагальнити можливості кожного з типу фільтрів.

5. Навести передатні характеристики цих фільтрів.

6. Як розташовані полюси фільтра Чебишева на еліпсі?

7. В чому відмінність розташування полюсів фільтра Чебишева від Батерворта?

8. Як можна визначити полюси фільтра Чебишева?

9. Порівняйте передаточні функції фільтрів Чебишева і Баттерворта.

10. В чому полягає відмінність Кауера у проектуванні аналогових фільтрів?

11. В чому полягає ефективність еліптичної апроксимації?

12. Як фазова не лінійність залежить від порядку фільтру?

13. Чим обумовлена групова затримка сигналів?

14. Навести приклади застосування фільтрів.

15. Зробіть порівняльний аналіз фільтрів Чебишева, Баттерворта та Кауера.