Рекурсивні фільтри з нескінченною імпульсною характеристикою

На відміну від КІХ НІХ-фільтри мають традиційні аналогові еквіваленти (фільтри Баттерворта, Чебишева, еліптичний і Бесселя) і можуть бути проаналізовані і синтезовані з використанням традиційних методів проектування фільтрів. НІХ-фільтри одержали таку назву, тому що їхні імпульсні характеристики розтягнуті на нескінченному часовому інтервалі. Це визначається тим, що дані фільтри є рекурсивними, тобто використовують зворотний зв'язок.

Хоча НІХ-фільтри можуть бути реалізовані з меншою, ніж КІХ-фільтри, кількістю обчислень, НІХ-фільтри не можуть мати таких характеристик, якими володіють КІХ-фільтри. Більш того, НІХ-фільтр не має лінійної фазової характеристики. Але обчислювальні переваги НІХ-фільтра губляться, коли вихідний сигнал фільтра піддається децимації, оскільки в цьому випадку всякий раз приходиться обчислювати заново значення вихідної величини.

Як правило НІХ-фільтри реалізуються за допомогою ланок другого порядку, що називаються біквадратними фільтрами, тому що описуються біквадратними рівняннями в z-області. Фільтри високого порядку проектують, використовуючи каскадування біквадратних ланок. Наприклад, фільтр шостого порядку вимагає трьох біквадратних ланок.

Характеристики рекурсивних фільтрів з нескінченною імпульсною характеристикою (НІХ):

- мають зворотний зв'язок (рекурсія);

- імпульсна характеристика має нескінченну тривалість;

- потенційно нестабільні;

- нелінійна фазочастотна характеристика;

- більш ефективні, ніж КІХ-фільтри;

- немає обчислювальних переваг при децимації по виходу;

- звичайно проектуються за характеристикою аналогового фільтра;

- як правило реалізуються каскадним з'єднанням ланок другого порядку (біквадратних фільтрів).

Загальне рівняння цифрового фільтра описує узагальнену передатну функцію H(z), що містить поліноми у чисельнику і знаменнику.

Структура біквадратного НІХ-фільтра. Нулі формуються коефіцієнтами прямого зв'язку b₀, b₁, b₂; а полюси (порядок) визначаються коефіцієнтами зворотного зв'язку 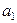і :

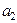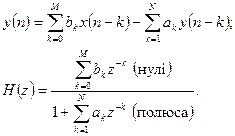
Хоча існує можливість створення безпосередньо за цим рівнянням НІХ-фільтра більш високого порядку (так звана пряма реалізація), але накопичення помилок квантування (через арифметику з фіксованою точкою і кінцевою довжиною слова) можуть викликати нестійкість роботи фільтра. З цієї причини практична реалізація виконується, як правило, каскадним включенням декількох біквадратних ланок з відповідними коефіцієнтами замість прямої форми реалізації.

Дані при обчисленні біквадратних фільтрів можуть масштабуватися роздільно, а потім біквадратні ланки каскадуються для мінімізації помилок квантування коефіцієнтів і помилок рекурсивного накопичення. Каскадні біквадратні фільтри працюють більш повільно, ніж їхні еквіваленти прямої форми реалізації, але вони, як правило, стійкі й у них мінімізуються ефекти, зв'язані з арифметичними помилками кінцевої розрядності даних.

Перша пряма форма біквадратної ланки вимагає використання чотирьох регістрів (рис. 9.7) і одного суматора.

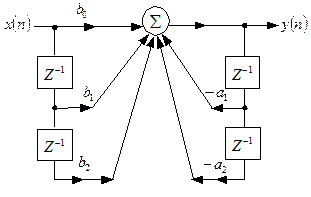
Рис. 9.7. — Апаратна реалізація НІХ-фільтра другого порядку
біквадратного (форма 1).

Ця конфігурація може бути замінена еквівалентною схемою, представленою на рис. 9.8, що називається другою прямою формою реалізації і вимагає використання тільки двох регістрів і двох додавачів. Можна показати, що рівняння, що описують біквадратний НІХ-фільтр другої прямої форми реалізації, такі ж, як і рівняння першої прямої форми реалізації. Як і у випадку КІХ-фільтра, система позначень при зображенні НІХ-фільтра часто спрощується.

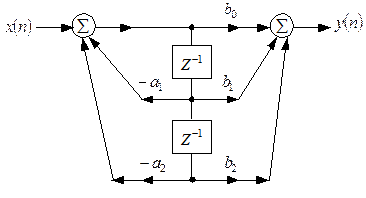
Рис. 9.8. — Апаратна форма реалізації біквадратного НІХ-фільтру
другого порядку (форма 2).

В цьому випадку необхідно виконати такі умови:

§ приводиться до такого ж рівняння, як для першої прямої форми;

§ ;

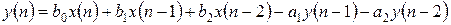§ вимагає тільки 2 елементи затримки (регістра).

Популярний метод проектування НІХ-фільтра зводиться до того, що спочатку проектується еквівалентний аналоговий фільтр, а потім функція передачі H(s) перетвориться за допомогою математичних перетворень в z-область, H(z). Проектування фільтрів більш високих порядків виконується каскадним включенням біквадратних ланок, що гарантує не тільки стійкість системи, але і задані динамічні властивості (утримання перерегулювання, коливальності за рахунок часу регулювання).

Методи проектування рекурсивних фільтрів

§ Метод інваріантості імпульсної характеристики:

¨ починається з визначення H(s) для аналогового фільтра;

¨ узяття зворотного перетворення Лапласа для одержання імпульсної характеристики;

¨ Одержання z-перетворення H(z) з дискретної імпульсної характеристики;

¨ z-перетворення визначає коефіцієнти фільтра;

¨ Повинний бути врахований ефект накладення спектрів.

§ Метод білінійного перетворення:

¨ інший метод для перетворення H(s) у H(z);

¨ характеристики визначаються диференціальним рівнянням, що описує аналогову систему;

¨ не важливий ефект накладення спектра.

§ Метод погодженого z-перетворення:

¨ відображає H(s) у H(z) для фільтрів і з полюсами, і з нулями.

§ Методи САПР:

¨ алгоритм Флетчера-Пауела;

¨ здійснюються каскадуванням біквадратних ланок.

Оцінка швидкості обробки даних при реалізації НІХ фільтрів:

§ визначення кількості біквадратних ланок, необхідних для реалізації бажаної частотної характеристики;

§ множення цієї кількості на час виконання операції однією біквадратною ланкою;

§ результат (плюс додаткові операції) визначає мінімально припустимий період дискретизації 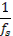для роботи в реальному масштабі часу.

Резюме: порівняння КІХ- і НІХ-фільтрів. Вибір між КІХ- і НІХ-фільтрами може бути свого роду змаганням у проектуванні, але кілька основних керівних принципів можна визначити. Як правило, НІХ-фільтри більш ефективні, чим КІХ-фільтри, тому що вони вимагають меншої кількості пам'яті і меншої кількості операцій множення з накопиченням. НІХ-фільтри можуть бути розроблені, ґрунтуючись на попередньому досвіді проектування аналогових фільтрів. НІХ-фільтри можуть приносити проблеми нестійкості, але цього не відбувається, якщо синтезовані фільтри високого порядку реалізуються як системи, що складаються з послідовного включення каскадів другого порядку.

З іншого боку, КІХ-фільтри вимагають більшої кількості ланок і, відповідно, операцій множення з накопиченням для реалізації частотної характеристики з заданою частотою зрізу, але при цьому мають лінійну фазову характеристику. КІХ-фільтри працюють на кінцевому часовому інтервалі даних, тому, якщо частина даних зіпсована (наприклад, у результаті збоїв у роботі АЦП), КІХ-фільтр буде "дзенькотіти" тільки на часовому інтервалі, що відповідає N–1 відлікам. НІХ-фільтр, через наявність зворотного зв'язку, буде "дзенькотіти" значно більш тривалий термін часу.

Рис. 9.9. — Порівняльний аналіз КІХ та НІХ фільтрів

Якщо необхідні фільтри з крутим спадом і відчувається дефіцит у часі, відведеному для обробки, найкращим вибором є еліптичний НІХ-фільтр. Якщо число операцій множення з накопиченням не є надмірним і потрібна лінійна фаза, то повинний бути обраний КІХ-фільтр. Якісний порівняльний аналіз НІХ і КІХ фільтрів наведений на рис. 9.9.