Рекурсивні обчислення, обчислення факторіалу, знаходження квадратного кореня методом ітерацій

Інший спосіб організації циклічних обчислень у мові Пролог пов’язаний із застосуванням рекурсії, яку використовують у ситуаціях, коли заздалегідь невідомо число елементів. Задача розбивається на тривіальні, граничні випадки та на загальні, через простіші.

Рекурсивне формулювання правила містить у своєму тілі посилання на заголовок цього самого правила. При описі рекурсії перше правило має задавати вихідне твердження. Класичним прикладом є означення поняття „предок” через поняття „батька”:

Предок (X, Z):- батько (X, Z),

Предок (X, Z):- батько (X, У),

предок (У, Z).

Предикати, що знаходяться правіше від рекурсивного виклику, не впливають на організацію рекурсії; вони виконуються лише після виходу з неї і набувають значення змінних із стеку, куди ці змінні попадають у ході рекурсії. Виконувані при цьому обчислення називають хвостовими. Рекурсія може потребувати багато системних ресурсів, оскільки у рекурсивному виклику нові копії використовуваних значень розміщуються в стеці і зберігаються там, доки правило не завершиться – успішно чи неуспішно. Використання ліворекурсивних правил, в яких рекурсивна ціль є першою в тілі правила, може породжувати нескінченні обчислення, до яких призводить також логічний круг в означенні. Наприклад:

батько (Х, У): - дитина (У, Х);

дитина (У,Х): - батько (Х, У).

Циклювання в процесі рекурсії викликає переповнення оперативної пам’яті та втрату цінної інформації. Корисним емпіричним правилом є введення перевірки перед кожною рекурсивною ціллю.

Розглянемо приклад організації мовою ПРОЛОГ рекурсивного обчислення факторіалу:

predicates

fact (integer, integer)

clauses
fact (0,1): - !.

fact (N,V): -

M=N-1,

fact (M,U),

V=U*N

goal
fact (3, X),

write („Факторіал 3 дорівнює”, Х), n1.

Виконання програми розпочинається з намагання досягти цілі fact (3, X), оскільки Х не визначено, предикат зводиться до fact (3, _). Його хвостова частина, оператор виведення, засилається до стеку. Далі здійснюється перехід на перший варіант однойменного правила: fact (0,1): -1. зіставлення для нього закінчується невдало (3<>1), обирається друге правило. При зіставленні аргументів здійснюється підстановка N=3, V=X, у процесі обробки тіла правила отримуємо N=2 і новий виклик fact (2,_), який не може бути виконано негайно, тому хвостова частина правила Х=U*3 засилається до стеку, здійснюється повернення до fact (0,1) і далі на fact (N,V) з новими значеннями N2=2, V2=U, відбувається невдалий виклик fact (1,_), хвостова частина правила у формі U=2* U2 записується до стеку. При новому поверненні предикат fact відкидається із значеннями N3=1, V3=U2, формується виклик fact (0,_), до стеку записується U2= U3*1. Тепер виявляється успішним перше правило, у результаті чого U3 набуває значення 1 і починається вивантаження стеку. При цьому послідовно формуються fact (1,1), fact (2,2), fact (3,6), потім здійснюється виведення результату. У першому твердженні відтинається другий варіант правила при зовнішньому запиті типу fact(0,Х):у протилежному випадку друге правило призведе до зациклювання під час обчислення факторіалу від від’ємних аргументів.

На рис. 8 показано графічну ілюстрацію обчислювальної частини описаного процесу. За намагання обчислення за цією програмою 8!=40320 результат виявляється від’ємним внаслідок переповнення розрядної сітки. Правильний результат можна отримати, замінивши тип відповідного параметра на дійсний.

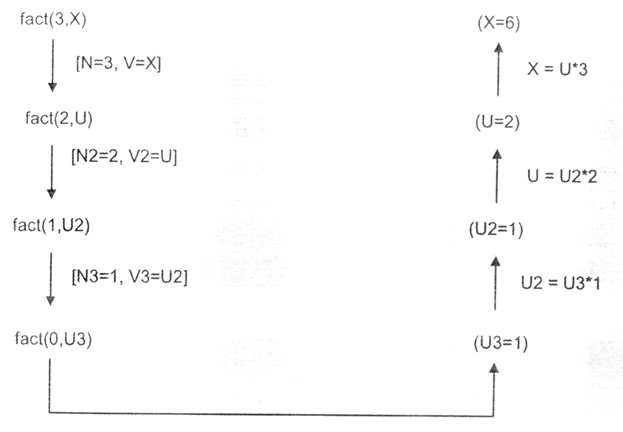
Рис.8. Процес обчислення факторіалу

Для розв’язання задачі знаходження квадратного кореня методом ітерацій використовується відома формула

.

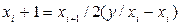Відповідна програма має вигляд:

clomains

r=real

predicates

root (r,r,r,r)

clauses

root (Y, X, EPS, Z): -

D=(Y/X-X)/2,

abs (D) >EPS,!,

X_i =X+D,

root (Y, X1, EPS, X1).

goal

root (0.49, 0, 6, 1e^-4, Z),

write (Z), n1.