Списки у мові Пролог, бінарні дерева

Однією з причин природності рекурсії у мові ПРОЛОГ є те, що дані часто мають рекурсивну структуру, список або порожній, або має голову і хвіст, який сам є списком у загальному випадку. Війкове дерево є або порожнім, або в нього є корінь і два піддерева, які самі є деревами.

Список задається переліком його елементів, вміщених у квадратні дужки, елементи списку можуть бути структурованими. Порядок слідування елементів є істотним, усі вони мають належати одному і тому самому домену, включно із списком структур.

Приклади списків:

[16, 24, 1, 6, 387, 0, 9]

[0,8, 168,45, 943,02, 681,8]

[„Колмановський Б.Д.”, „Петров Л.Є.”, „Сидоров Л.С.”]

Порожній список позначається [].

Щоб використати списки у ПРОЛОГ-програмі, необхідно спочатку в розділі clomains описати домени списку у форматі

<ім’я _домену>=<тип_елементу>*

Наприклад, домен списку з цілочисловими елементами описується як

domains

list_num=integer*

Потім у секції predicates необхідно описати предикат, що працює зі списком.

Наприклад:

predicates

num (list_num)

Сам список вводиться у розділах goal чи clauses.

Головою списку вважається перший елемент, уся інша частина, отримана „утинанням глави”, пов’язана з хвостом. Операція поділу списку на голову та хвіст позначається І. Запис [НІТ] можна розглядати також як новий список, у якому елемент Н добавлено у голову списку Т. Імена для частин списку можна вибирати довільно. Типовими задачами обробки списків є:

1) перевірка належності до списку;

2) вибір елементу списку;

3) поділ списку;

4) стикування списків;

5) вибір максимуму чи мінімуму;

6) сортування.

Приклад програми приєднання списку L2 до кінця списку L1:

domains

lint=integer*

int=integer

predicates

append (lint, lint, lint)

clauses

append ( [], L, L),

append ( [N|L1], L2, [N|] ) : -

/Голова L1пересилається до L3*/

append ([1, 2, 3], [4, 5], X),

write (X).

Нехай на вхід надійшли списки L1=[1, 2, 3], L2=[4, 5]. Спочатку предикат має вигляд ([1, 2, 3], [4, 5], [ ]). Пролог, діючи за другим правилом, буде виштовхувати черговий елемент першого списку до стеку, до вичерпування цього списку. Потім починає діяти перше правило. Третій список ініціалізується другим і виходить append ([ ], [4, 6], [4, 5]). Далі знову за другим правилом до першого і третього списків приписується вершина стеку. Процес закінчується досягненням ситуації ([1, 2, 3], [4, 5], [1, 2, 3, 4, 5]).

Теорія графів (деревовидних графів) має різне застосування в галузях інформатики. Кожній вершині дерева можна поставити у відповідність список безпосередніх спадкоємців. Особливо зручною у мові Пролог є робота з бінарними деревами. Бінарне дерево визначається рекурсивно, як таке, що має ліве піддерево Л, корінь К та праве піддерево П. Такі дерева можна подати термінами bintree (Л, К,П) Відсутні піддерева позначаються стандартним терміном nil. Тоді дерево (рис.) можна зобразити конструкцією

bintree (bintree (nil, d, nil), b, bintree (nil, e, nil)),

a

bintree (nil, c, f)/

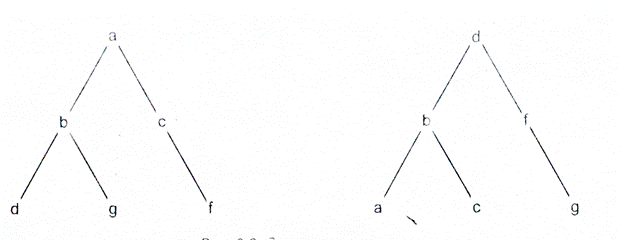
Рис.9 Двійкове дерево

Зображення впорядкованої множини бінарним деревом дає змогу суттєво прискорити вибірку її елементів. Дерево має бути впорядкованим так, щоб будь-який елемент у лівому піддереві був меншим кореня, а в правому – більшим. Тоді можна записати в Пролог-програмі перевірки належності елемента дереву:

intree (X, bintree (LF, X, RG)). /*Якщо Х – корінь*/

intree (X, bintree (LF, Y, RG)): - /*Якщо Х більше кореню*/

X@<Y, ↓

intree (X, RG) /*і міститься в правому*/

intree (X, bintree (LF, Y, RG)): -

X@<Y, /*Якщо Х менше кореня*/

intree (X, LF) /*і міститься в лівому*/

Комбінація типу @ означає порівняння кодів символів-операндів. Самі елементи можуть бути складеними і містити інформаційні поля. Вибір елементу відкриває доступ до інформації, що міститься в них. Для роботи з бінарними деревами необхідні додаткові процедури впорядкування лінійного списку, перетворення списку у бінарне дерево і навпаки, додавання елементу до дерево видного списку.