Задачі класифікації, експертні системи

Особливий клас систем ШІ становлять експертні системи (ЕС), що включають знання спеціалістів про певну слабко структуровану, важко формалізовану вузьку галузь і здатні у цій галузі пропонувати і пояснювати розумні рішення. Їх основним призначенням є:

1) інтерпретація даних (наприклад, визначення структури хімічних з’єднань, мінералів, комах та рослин, класифікація типу особи за результатами тестування);

2) діагностика станів технічного пристрою чи хворого;

3) моніторинг (спостереження за процесом та сигналізація про аномалії);

4) прогнозування імовірного розвитку подій (погоди, врожаю, економічні кон’юнктури);

5) планування послідовності дій для досягнення цілі;

6) навчання майбутніх спеціалістів.

Усі ці задачі зводяться до розпізнавання образів.

Задача класифікації полягає в групуванні об’єктів у певне скінчене число класів {l₁, l₂, …l_n}. Зіставлення опису образу об’єкта з правилами визначення належності до класу називається розпізнаванням образу. Названі процеси можуть бути імовірнісними та адаптивними. В останньому випадку алгоритму подаються достовірно розпізнавані об’єкти, і він автоматично уточнює правила класифікації. У найбільш розвинених системах реалізуються так звані генетичні алгоритми самонавчання з випадковими „мутаціями” класифікаційних правил та відбором корисних мутацій.

Байєсівські правила базуються на апостеріорному (спостереження події B_j) перерахунку імовірностей гіпотез {Ai} про належність об’єкта до взаємовиключних класів:

Ці правила потребують великого обсягу навчальної інформації. Розв’язок зазвичай приймається за мінімумом очікуваного ризику, якщо він великий, то експерименти можна продовжити.

Центральною проблемою логічного виведення лишається проблема перебирання великої кількості варіантів, який важко припускає розподіл. Геометричний підхід переводить задачу формування знань на мову геометричних співвідношень між емпіричними фактами, які зображуються точками в просторі ознак. Правила входження об’єктів до певних класів еквівалентності базуються на основі відповідних „відстаней”, як правило, зважених. Ситуація піддається природній візуалізації.

Якщо описи об’єктів можна зобразити у вигляді точок у метричному, зокрема евклідовому, просторі, то точка, що розпізнається, відноситься до найближчого за відстанню класу. У більш загальному випадку будуються системи функцій 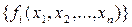, і об’єкт відноситься до класу, і якщо за умови підстановки його координат і-та функція отримує найбільше значення.

Найбільш зручними для процесів розпізнавання та навчання є лінійні класифікаційні процедури, які зводяться до обчислення скалярних добутків 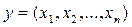на стрічці класифікаційної матриці.

При розпізнаванні зорових образів насамперед намагаються визначити їх форму як властивість, інваріантну до перетворень подібності (масштабування, обертання та зсув лишають квадрат квадратом і не мають форму трикутника). На основі цієї ідеї та груп перетворень, що не виводять об’єкт з вихідного класу, можна побудувати скінчене число еталонів, наближено, з врахуванням цих перетворень, що покривають цю предметну область.

Для складових об’єктів звичайно застосовуються багаторівневі процедури, які базуються на апараті формальних граматик. Задача розпізнавання деталей на зображеннях складових просторових об’єктів ускладнюється внаслідок часткового перекриття їх зображень. У цьому випадку для розпізнавання об’єктів заднього плану використовуються зрізані еталони.