Структура системи цифрової обробки аналогових сигналів

Цифрова фільтрація є одним з сучасних інструментальних засобів обробки результатів вимірювань. Крім переваг усунення помилок, пов'язаних із флуктуаціями параметрів пасивних компонентів за часом і за температурою, дрейфом операційного підсилювача і т.д., цифрові фільтри здатні задовольняти таким технічним вимогам за своїми параметрами, яких, у кращому випадку, було б надзвичайно важко або навіть неможливо досягти в аналоговому виконанні. Характеристики цифрового фільтра можуть бути легко змінені програмно. Вони широко використовуються в вимірювальних системах, томографічних комплексах, телекомунікаціях, у додатках адаптивної фільтрації, таких як придушення відлуння, шуму. Процес проектування цифрових фільтрів складається з тих же етапів, що і процес проектування аналогових фільтрів. Спочатку формулюються вимоги до бажаних характеристик фільтра, по яких потім розраховуються параметри фільтра. Амплітудна і фазова характеристики формуються аналогічно аналоговим фільтрам. Ключове розходження між аналоговим і цифровим фільтрами полягає в тім, що, замість обчислення величин опорів, ємностей і індуктивностей для аналогового фільтра, розраховуються значення коефіцієнтів для цифрового фільтра. Ці числа є коефіцієнтами фільтра, вони постійно знаходяться в пам'яті і використовуються для обробки дискретних даних.

Цифровий фільтр, що працює в реальному масштабі часу, оперує з дискретними за часом і за рівнем даними записаними в вигляді коду. Черговий відлік, що відповідає реакції фільтра формується на закінченні кожного періоду дискретизації. Внаслідок дискретної природи сигналу, на відліки даних найчастіше посилаються за їхніми номерами, наприклад, відлік 1, відлік 2, відлік 3 і т.д. На відміну від попередніх, розглянемо задачі фільтрації, коли спектри сигналу і завади мають різний частотний діапазон. Спочатку відбувається оцифрування сигналу за допомогою АЦП (за часом, за рівнем і перетворюється в код) для одержання вибірки x(n) (рис. 9.1). Вона надходить до цифрового НЧ фільтру. Відліки вихідних даних y(n) використовуються для відновлення аналогового сигналу з використанням ЦАП. Для роботи в реальному масштабі часу процесор повинний бути розрахований на виконання всіх кроків у програмі фільтрації в межах проміжку часу, що відповідає одному такту дискретизації. Високопродуктивний універсальний процесор з фіксованою точкою, здатний виконати операцію множення з накопиченням (при реалізації одного каскаду фільтра) за 13,3 нс. Наприклад, для 100-каскадного фільтра повний час обчислення складає приблизно 1,4 мкс. Це відповідає максимально можливій частоті дискретизації 714 кГц, обмежуючи ширину смуги частот оброблюваного сигналу декількома сотнями кілогерц.

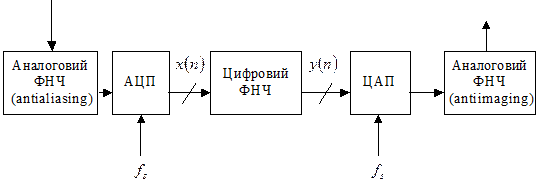
Рисунок 9.1 — Схема цифрової фільтрації

У дискретних системах, навіть з високим ступенем надлишкової дискретизації, потрібні аналогові ФНЧ перед АЦП і після ЦАП для усунення ефекту накладення спектрів. З ростом частоти сигнали виходять за рамки можливостей АЦП, і цифрова фільтрація стає неможливою. Але на дуже високих частотах і аналогова фільтрація теж неможлива через обмеження, які зв'язані зі смугою пропускання і спотвореннями операційних підсилювачів. Фільтри для роботи в реальному масштабі часу можуть бути реалізовані програмно на персональних комп'ютерах та мікропроцесорах.

Якісний порівняльний аналіз аналогових і цифрових фільтрів вимірювальних електронних систем наведено на рис. 9.2.

У більшості сучасних систем обробки сигналів використовуються комбінації аналогових і цифрових методів для реалізації бажаних функцій і використовуються переваги всіх методів, як аналогових, так і цифрових.

Вимоги до цифрової фільтрації для роботи в реальному масштабі часу:

§ смуга сигналу = ;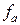

§ частота дискретизації ;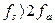

§ період дискретизації = ;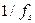

§ час обчислення фільтра + додаткові операції < період дискретизації:

¨ залежить від числа коефіцієнтів фільтра;

¨ швидкості операцій множення з накопиченням;

¨ ефективності цифрової обробки сигналів (ЦОС):

· підтримка циклічних буферів;

· відсутність додаткових операцій.

Рис. 9.2 — Порівняння цифрових і аналогових фільтрів

Існує два основних типи цифрових фільтрів: нерекурсивні фільтри з кінцевою імпульсною характеристикою (КІХ) і рекурсивні (зі зворотним зв'язком) фільтри з нескінченною імпульсною характеристикою (НІХ).

Змінюючи ваги коефіцієнтів і число ланок КІХ-фільтра, можна реалізувати практично будь-яку частотну характеристику. КІХ-фільтри можуть мати такі властивості, що неможливо досягти методами аналогової фільтрації. Але високоефективні КІХ-фільтри будуються з великим числом операцій множення з накопиченням і тому вимагають використання швидкодіючих процесорів.

НІХ-фільтри мають тенденцію імітувати принцип дії традиційних аналогових фільтрів зі зворотним зв'язком. Тому їх імпульсні характеристики мають нескінченну тривалість. Завдяки використанню зворотного зв'язку НІХ-фільтри можуть бути реалізовані зі значно меншою кількістю операцій (коефіцієнтів), ніж КІХ-фільтри.

Іншим способом реалізації КІХ- чи НІХ-фільтрації є ґратчасті фільтри. Цифрові фільтри застосовуються в додатках адаптивної фільтрації.

Типи цифрових фільтрів зводяться до наступних.

- Фільтр ковзного середнього (КІХ).

§ Фільтр із кінцевою імпульсною характеристикою (КІХ):

¨ лінійна фаза;

¨ простота проектування;

¨ значні обчислювальні витрати.

§ Фільтр із нескінченною імпульсною характеристикою (НІХ):

¨ висока обчислювальна ефективність;

¨ засновані на класичних аналогових фільтрах.

§ Ґратчасті фільтри (можуть бути КІХ чи НІХ).

§ Адаптивні фільтри.