Огляд популярних аналогових фільтрів
Найбільш популярними аналоговими фільтрами є фільтри Баттерворта, Чебишева, Чебишева-Кауера-Золотарьова і Бесселя. Існує безліч програм САПР, здатних генерувати функцію передачі фільтра, задану за допомогою перетворення Лапласа.
Фільтр Баттерворта, що не має нулів частотної характеристики, (також називаний фільтром з максимально плоскою характеристикою), не створює пульсацій (нерівномірності) у смузі пропускання й у смузі затримки, тобто має монотонну характеристику в обох смугах.
Фільтр Чебишева 1-го роду має більш швидкий спад частотної характеристики, ніж фільтр Баттерворта (при однаковому порядку), і створює пульсації (нерівномірність) у смузі пропущення. Рідше використовуються фільтри Чебишева 2-го роду, що мають пульсації (нерівномірність) у смузі затримки, а не в смузі пропускання.
Еліптичний фільтр (фільтр Чебишева-Кауера-Золотарьова) має полюси і нулі частотної характеристики і створює пульсації (нерівномірність) як в смузі пропускання, так і в смузі затримки. Цей фільтр має більш швидкий спад частотної характеристики, ніж фільтр Чебишева при тім же числі полюсів (порядку). Еліптичний фільтр часто використовується там, де допускається трохи гірша фазова характеристика, хоча належним вибором координат нулів її можна суттєво скорегувати.
Нарешті, фільтр Бесселя (Томпсона), що не має нулів частотної характеристики, володіє оптимальною імпульсною характеристикою і лінійною фазовою характеристикою, але має гірший спад частотної характеристики з усіх типів фільтрів, що обговорювалися, при тім же числі полюсів (порядку).
Розглянені переваги фільтри, які являються основними, а саме:
§ Баттерворта:
§ немає нулів частотної характеристики, немає пульсацій у смузі пропускання і затримки;
§ максимально плоска характеристика (швидкий спад без пульсацій).
§ Чебишева 1-го роду:
¨ немає нулів частотної характеристики, пульсації в смузі пропускання, немає пульсацій у смузі затримки;
¨ більш коротка область переходу, ніж у фільтра Баттерворта для даного порядку;
¨ фільтр 2-го роду має пульсації в смузі затримки, немає пульсацій у смузі пропускання;
¨ Еліптичний (Чебишова-Кауера-Золотарьова):
¨ має полюси і нулі, пульсації й у смузі пропускання, і в смузі затримки;
¨ більш коротка область переходу, ніж у фільтра Чебишева для даного порядку;
¨ фазова характеристика гірше.
¨ Бесселя (Томпсона):
¨ немає нулів частотної характеристики, немає пульсацій у смузі пропускання і затримки;
¨ оптимізований за лінійною фазовою характеристикою;
¨ сама довга перехідна характеристика з усіх фільтрів даного порядку.
Усі перераховані вище типи аналогових фільтрів описані в літературі. Їх цифрова реалізація передбачає z-перетворення. Існує три методи перетворення зображення за Лапласом в z-зображення:
- метод інваріантості імпульсної характеристики;
- білінійне перетворення;
- погоджене z-перетворення.
Результуюче z-зображення може бути перетворене в коефіцієнти біквадратного НІХ-фільтра. Підхід САПР при проектуванні НІХ-фільтра подібний програмі Паркса-Маккліллана, використовуваної для КІХ-фільтрів. Ця методика використовує алгоритм Флетчера-Пауела (Fletcher-Powell). Для одержання вихідного відліку біквадратного фільтра при його реалізації потрібно сім командних циклів 93 нс, що визначає максимально можливу частоту дискретизації.
Оскільки фільтрація сигналів являє собою важливу технічну проблему, їй була приділено серйозна увага і знайдена, що ряд апроксимацій характеристик фільтра, відрізняються особливо задовільними якостями. Нижче перераховані деякі з розповсюджених типів фільтрів:
1) Фільтр Баттерворта з монотонною убутною плоскою амплітудно-частотною характеристикою при 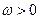
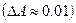 ;
;
2) Фільтр Чебишева з рівнохвильовою у смузі прозорості і монотонно убутною в смузі затримання амплітудно-частотною характеристикою 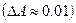 ;
;
3) Інверсний фільтр Чебишева з монотонно убутною в смузі прозорості 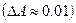 і рівнохвильовою у смузі затримання амплітудно-частотною характеристикою;
і рівнохвильовою у смузі затримання амплітудно-частотною характеристикою;
4) Еліптичний фільтр із рівнохвильовою як у смузі прозорості, так і в смузі затримання амплітудно-частотною характеристикою;
5) Фільтр Бесселя, що побудований на основі апроксимації поруч Тейлора поблизу s=0 лінійної фазочастотною характеристики.
Дата добавления: 2015-06-27; просмотров: 751;
