Порівняльний аналіз амплітудних і фазових характеристик фільтрів Баттерворта, Чебишева та еліптичного.
Для порівняння характеристик фільтрів розрахуємо передатніхарактеристики фільтрів Баттерворта, Чебишева й еліптичного для поставленої задачі.
Фільтр Баттерворта
Функція Баттерворта n-го порядку визначається в наступному виді:
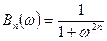 ,
, 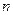 =1, 2, … (8.2)
=1, 2, … (8.2)
Розрахунок коефіцієнтів поліномів ведеться з прагнення апроксимувати максимально плоску АЧХ фільтру, яка при нормуванні, описується функцією:
|W(jw)|=(w2n-1)1/2
де: w=w/wср - відносна частота; wср - частота зрізу;
n - порядок фільтру.
Внаслідок зростання порядку n фільтра Баттерворта коефіцієнт передачі в смузі прозорості в більшому ступені наближається до одиниці, перехідна область усе в більшому ступені звужується, а в смузі затримання функція передачі все ближче і ближче підходить до нуля. Таким чином, n є параметром, вибір якого дозволяє задовольнити заданий вибір вимог до фільтра як в смузі прозорості так і в смузі затримання. Оскільки проектується фільтр із нерівномірністю в смузі прозорості 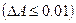 , значить порядок фільтра повинний бути не менше n=6. В процесі проектування через похибки обчислень характеристики фільтра будуть погіршуватися, тоді раціонально прийняти порядок фільтра n=8.
, значить порядок фільтра повинний бути не менше n=6. В процесі проектування через похибки обчислень характеристики фільтра будуть погіршуватися, тоді раціонально прийняти порядок фільтра n=8.
Наведемо поліноми нормованих фільтрів Баттерворта першого. другого, третього та четвертого порядків, відповідно 1+р; 1+2´0,707р+р2; (1+р)(1+2´0,5р+р2); ( 1+ 2´0,3825р + р2)(1+2´0,924 р + р2).
Полюси функції Баттерворта нормованого фільтра нижніх частот розташовані на колі одиничного радіуса в s-площині. Коли шкала частоти фільтра нижніх частот вибирається з таким розрахунком, що його частота зрізу складає 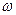 рад/с, а не 1 рад/с полюси переміщуються уздовж радіальних ліній до відповідних крапок на колі радіусу wc.
рад/с, а не 1 рад/с полюси переміщуються уздовж радіальних ліній до відповідних крапок на колі радіусу wc.
Знаходимо полюси необхідної передатної функції. Полюси розташовані в лівій і правій напівплощинах визначаються наступними вираженнями:
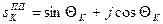 , (8.3)
, (8.3)
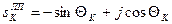 , (8.4)
, (8.4)
де 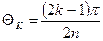 , а
, а 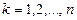 .
.
Графік розташування полюсів на комплексній s-площині показаний на рисунку 8.3.
Координати полюсів для полінома Баттерворта 8-го порядку приведені в таблиці 8.1.
Таблиця 8.1. – Координати полюсів для полінома Баттерворта
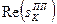
| 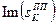
| 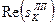
| 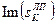
|
| -0,195 | 0,981 | 0,195 | 0,981 |
| -0,556 | 0,831 | 0,556 | 0,831 |
| -0,831 | 0,556 | 0,831 | 0,556 |
| -0,981 | 0,195 | 0,981 | 0,195 |
| -0,981 | -0,195 | 0,981 | -0,195 |
| -0,831 | -0,556 | 0,831 | -0,556 |
| -0,556 | -0,831 | 0,556 | -0,831 |
| -0,195 | -0,981 | 0,195 | -0,981 |
 |
Рис. 8.3. – Розташування полюсів на комплексній s-площині.
Для розрахунку фільтра ми будемо використовувати полюси тільки з лівої (стійкої) частини s-площини, відкидаючи полюси, що лежать у правій (хитливій) частині комплексної s-площини.
Передатна функція нормованого фільтра нижніх частот для випадку, коли n – парне:
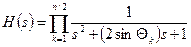 . (8.5)
. (8.5)
Підставляючи в (8.5) знайдені значення і спрощуючи вираження, ми одержимо необхідну передатну функцію нормованого фільтра Баттерворта нижніх частот 8-го порядку:
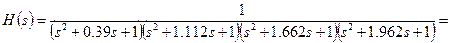
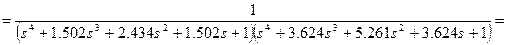
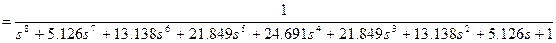 (8.6)
(8.6)
Фільтр, подібний до фільтра Баттерворта, у якому всі ступені свободи використовуються одержання амплітудно-частотної характеристики з плоскою ділянкою на початку координат, може виявитися не кращим рішенням.
На рисунку 8.4 приведені амплітудно-частотні характеристики нормованих фільтрів нижніх частот 8-го і 16-го порядків.
Рис. 8.4 – Амплітудно-частотні характеристики нормованого фільтра Баттерворта нижніх частот 8-го (RH(w)) і 16-го (RH2(w)) порядків.
 |
Рис. 8.4 -Нормований фільтр Чебишева.
У багатьох випадках важливіше мати апроксимацію, що має рівномірно гарну якість на протязі усієї смуги прозорості. Таким фільтром, що має подібні рівномірні апроксимуючі властивості, є фільтр Чебишева.
Розрахунок коефіцієнтів поліномів ведеться з прагнення апроксимувати АЧХ фільтру з максимальним придушенням. Якнайкраща апроксимація описується функцією:
|W(jw)|2=1/(1+e2Tn2(w))
де: e - постійний коефіцієнт, що визначає нерівномірність АЧХ фільтру;
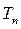 - поліном Чебишева першого роду n-го порядку.
- поліном Чебишева першого роду n-го порядку.
У смузі пропускання квадрат АЧХ |W(jw)|2 фільтру коливається між рівнями, рівними 1 і 1/(1+e2), причому число таких коливань ("хвиль" на графіку АЧХ) тим більше, чим вище порядок n фільтру. Амплітуда цих коливань однакова.
Як і у випадку фільтра Баттерворта передатна функція фільтра Чебишева має одні тільки полюси – чисельників її представляє постійну величину і, отже, не містить нулів при кінцевих значеннях частоти. Полюси фільтра Чебишева розташовуються на еліпсі, а не на колі, як у випадку фільтра Баттерворта. Велика вісь цього еліпса проходить по уявній осі s-площини, тоді як мала вісь – уздовж дійсної осі. Чим вужче еліпс, тим ближче розташовуються полюси до уявної осі і, отже, тим більше сильний вплив буде робити кожен полюс, тобто тим помітніше будуть коливання частотної характеристики. Таким чином, задана величина нерівномірності передачі вплине на розташування полюсів результуючої передатної функції, причому, чим більше нерівномірність, тим вужче виглядає еліпс.
Полюси передатної функції фільтра Чебишева визначаються через комплексну перемінну 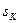 , яку ми знаходимо з вираження:
, яку ми знаходимо з вираження:
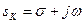 , (8.7)
, (8.7)
де 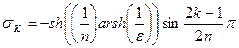 ;
;
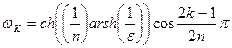 ;
;
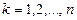 .
.
Коливальний параметр 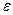 визначається виходячи з максимальної величини відносного загасання
визначається виходячи з максимальної величини відносного загасання 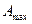 , дБ у смузі прозорості:
, дБ у смузі прозорості:
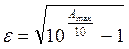 . (8.8)
. (8.8)
 |
У нашому випадку для
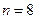 ,
, 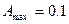 дБ розташування полюсів показане на рис. 8.5.
дБ розташування полюсів показане на рис. 8.5.
Рис. 8.5 – Розташування полюсів фільтра Чебишева 8-го порядку.
Координати полюсів для фільтра Чебишева 8-го порядку приведені в таблиці 8.2.
Таблиця 8.2. – Координати полюсів для фільтра Чебишева 8-го порядку
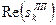
| 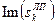
| 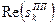
| 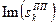
|
| -0,035 | 0,996 | 0,035 | 0,996 |
| -0,1 | 0,845 | 0,1 | 0,845 |
| -0,149 | 0,564 | 0,149 | 0,564 |
| -0,176 | 0,198 | 0,176 | 0,198 |
| -0,176 | -0,198 | 0,176 | -0,198 |
| -0,149 | -0,564 | 0,149 | -0,564 |
| -0,1 | -0,845 | 0,1 | -0,845 |
| -0,035 | -0,996 | 0,035 | -0,996 |
Для побудови передатної функції 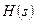 використовуються співмножники, зв'язані з полюсами, що розташовані в лівій (стійкої)
використовуються співмножники, зв'язані з полюсами, що розташовані в лівій (стійкої) 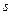 -напівплощини. Таким чином, передатна функція нормованого фільтра Чебишева нижніх частот визначається вираженням:
-напівплощини. Таким чином, передатна функція нормованого фільтра Чебишева нижніх частот визначається вираженням:
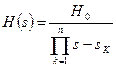 (8.9)
(8.9)
де 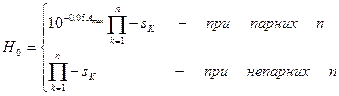 .
.
Підставляючи в (8.9) отримані дані і спрощуючи вираження, ми одержимо необхідну передатну функцію нормованого фільтра Чебишева нижніх частот 8-го порядку:
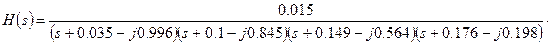
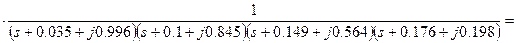
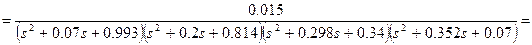
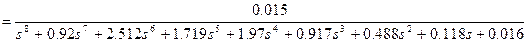 . (8.10)
. (8.10)
Вид амплітудно-частотних характеристик нормованого фільтра Чебишева нижніх частот 8-го і 16-го порядків приведений на рисунку 8.6.
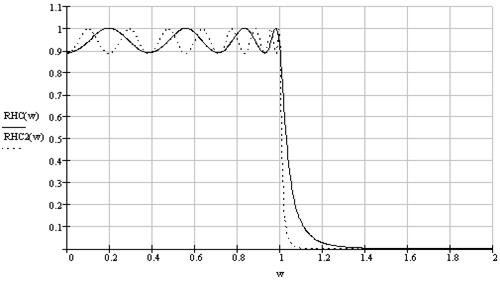
Рис. 8.6. - Амплітудно-частотні характеристики нормованого фільтра Чебишева нижніх частот 8-го (RH(w)) і 16-го (RH2(w)) порядків.
У інверсному фільтрі Чебишева АЧХ монотонно змінюється в смузі пропускання і пульсує в смузі загороди. Апроксимація АЧХ описується функцією:
|W(jw)|2 = e2Tn2(jw) / (1+e2Tn2(jw))
У смузі загороди квадрат АЧХ |W(jw)|2 фільтру коливається між значеннями 0 і e2/(1+e2)
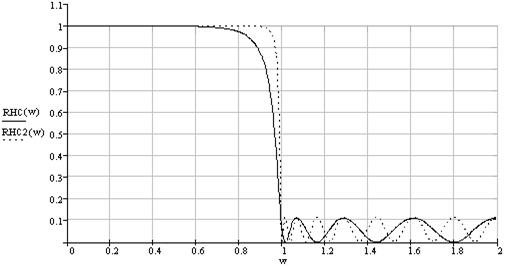
Рис. 8.7 - Амплітудно-частотні характеристики інверсного фільтра Чебишева нижніх частот 8-го (RH(w)) і 16-го (RH2(w)) порядків.
Дата добавления: 2015-06-27; просмотров: 883;
