Нерекурсивні фільтри з кінцевою імпульсною характеристикою

Елементарною формою КІХ-фільтра є фільтр ковзного середнього (moving average), який використовується для згладжування даних, наприклад, для аналізу математичного очікування випадкового сигналу. Вхідні відліки x(n) пропускаються через ряд регістрів пам'яті (позначених z-1 відповідно до представлення елемента затримки).

Розглянемо приклад, де є чотири каскади, що відповідають 4-точковому фільтру ковзного середнього. Кожен відлік збільшується на 0,25, і результати множення додаються для отримання значення ковзного середнього. Першим кроком є запам'ятовування перших чотирьох відліків x(0), x(1), x(2), x(3) у регістрах. Ці величини складаються і потім перемножуються на 0,25 для одержання першого виходу y(3). Початкові значення виходів y(0), y(1), y(2) некоректні, тому що, поки відлік x(3) не отриманий, ще не всі регістри заповнені. Коли отримали відлік x(4), він додається до результату, а відлік x(0) віднімається від результату. Потім новий результат повинний бути помножений на 0,25. Тому обчислення, необхідні для одержання нового значення на виході, складаються з одного додавання, одного віднімання та одного множення, незалежно від довжини фільтра ковзного середнього.

Схема узагальненого КІХ-фільтра наведена на рис. 9.3.

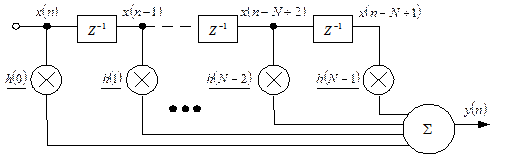
Рис. 9.3 — Узагальнений нерекурсивний фільтр з кінцевою
імпульсною характеристикою (КІХ)

Для N-точкового фільтру ковзного середнього .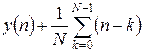

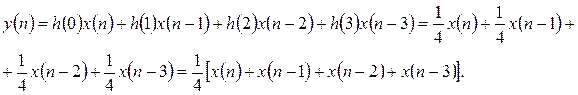
Фільтр ковзного середнього не має викиду за фронтом вхідного сигналу. Це робить його особливо корисним у додатках обробки сигналів, де потрібна фільтрація випадкового білого шуму при збереженні характеру вхідного імпульсу. З усіх можливих лінійних фільтрів фільтр ковзного середнього дає самий низький рівень шуму при заданій крутості фронту імпульсу.

Приклад обчислення вихідного сигналу.

;

;

;

;

.

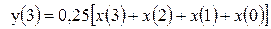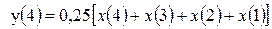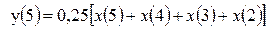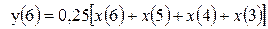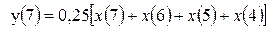Рівень шуму знижується при збільшенні числа точок. Істотно, що час реакції фільтра на східчастий вплив від 0 % до 100 % дорівнює добутку загальної кількості точок фільтра на період дискретизації.

Частотна характеристика простого фільтра ковзного середнього виражається дуже поширеною в інженерних додатках функцією sin(x)/x. Збільшення числа точок звужує основний пелюсток, але істотно не зменшує амплітуду бічних пелюстків частотної характеристики, що дорівнює приблизно –14 дБ для фільтра з 11- і з 31-відліками. Природно, такі фільтри не підходять у тім випадку, де потрібно велике ослаблення сигналу в смузі затримання. Крутість спаду може бути досягнена збільшенням кількості ланок фільтра, а характеристики смуги загасання поліпшуються вибором коефіцієнтів фільтру.

На відміну від фільтру ковзного середнього, для реалізації кожної ступені узагальненого КІХ-фільтру потрібен цикл множення з накопиченням. Схему КІХ фільтра можна спростити, що показано на рис. 9.4.

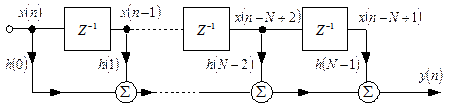
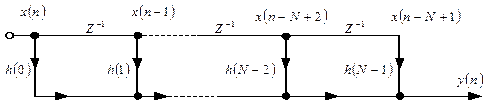
Рис. 9.4 — Спрощена схема фільтра

Фільтр з кінцевою імпульсною характеристикою описується лінійним рівнянням:

,

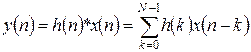де 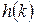— масив коефіцієнтів фільтра;

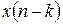— вхідний масив даних фільтра;

* — символ згортки.

Потрібне число N операцій множення з накопиченням виконується для кожного вихідного відліку, визначає число ланок і ефективність фільтра. КІХ-фільтр із числом ланок N вимагає N циклів (операцій) множення з накопиченням коефіцієнтів і необхідного числа ланок при формуванні бажаної частотної характеристики фільтра H(f). Для включення необхідної частотної характеристики H(f) у набір КІХ-коєфіціентів використовуються різні алгоритми і програмні пакети. Більшість цих програмних забезпечень розроблено для персональних комп'ютерів, які доступні на ринку послуг.

Обмеження на число ланок фільтра визначається насамперед терміном процесорного циклу, частотою дискретизації і необхідним обсягом обчислень. Наприклад, для КІХ-фільтра 100 порядку обчислення виконується за 1,4 мкс.

Псевдокод програми фільтра з циклічною буферизацією включає.

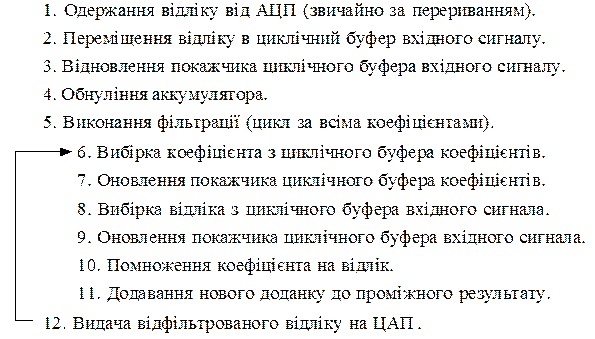
Ключовою теоремою проектування КІХ-фільтра є твердження, що коефіцієнти H(f) КІХ-фільтра є просто квантованими значеннями імпульсної характеристики цього фільтра. Відповідно, імпульсна характеристика є дискретним перетворенням Фур'є від H(f).

Завдяки сучасним засобам САПР, проектування КІХ-фільтрів виконується відносно просто. На вхід КІХ-фільтра подається одиночний імпульс, і в міру проходження цього імпульсу через елементи затримки, на виході по черзі формуються коефіцієнти фільтра. Таким чином, процес проектування КІХ-фільтра складається у визначенні його імпульсної характеристики за бажаною частотною характеристикою з наступним квантуванням імпульсної характеристики в ході генерації коефіцієнтів фільтра.

Корисно проаналізувати співвідношення між часовим і частотним представленнями для кращого розуміння принципів, що лежать в основі цифрових фільтрів (рис. 9.5). У дискретній системі операція згортки може бути представлена низкою операцій множення з накопиченням. Операція згортки в часовій чи частотній області еквівалентна множенню "точки на точку" у відповідній дуальній області.

Рис. 9.5. — Подвійність (дуальність) часу і частоти.

Наприклад, згортка в часовій області еквівалентна множенню в частотній області. Очевидно, що фільтрація в частотній області може бути виконана множенням на 1 усіх частотних компонентів у смузі пропускання і множенням на 0 усіх частотних компонентів у смузі затримання. І навпаки, згортка в частотній області еквівалентна множенню "точки на точку" у часовій області.

Основні характеристики КІХ-фільтрів.

§ Імпульсна характеристика має кінцеву тривалість (N циклів).

§ Лінійна фаза, постійна групова затримка (N непарне).

§ Немає аналогового еквівалента.

§ Безумовна стійкість.

§ Може бути адаптивним.

§ Обчислювальні переваги при децимації на виході.

§ Легке розуміння принципів і проектування.

Методи проектування КІХ-фільтрів виконуються таким чином:

- віконний метод sin(x)/x (Windowed-Sinc);

- розкладання в ряд Фур'є зі зважуванням (Windowing);

- синтез довільної частотної характеристики і використання зворотного швидкого перетворення Фур'є (ШПФ);

- програма Паркса-Маккліллана (Parks-Mаcсlellan) з алгоритмом обміну Ремеза (Remez).

Функція передачі в частотній області (1 чи 0) може бути відображена в часову область з використанням дискретного перетворенням Фур'є (ДПФ). В часовій області це дає імпульсну характеристику фільтра. Тому що множення в частотній області (спектр сигналу збільшується на функцію передачі фільтра) еквівалентно згортці в часовій області (сигнал згорнутий з імпульсною характеристикою), то сигнал може бути відфільтрований шляхом обчислення його згортки з імпульсною характеристикою фільтра. Задача фільтрації з використанням КІХ-фільтра є в точності таким процесом.

Оскільки ми маємо справу з дискретною системою, сигнал і імпульсна характеристика квантуються за часом і амплітудою, даючи в результаті набір дискретних відліків. Дискретні відліки, що включають бажану імпульсну характеристику, є коефіцієнтами КІХ-фільтра. Математичний апарат, застосовуваний при проектуванні фільтрів (аналогових чи цифрових), в основному базується на перетвореннях Фур'є. У неперервних за часом системах як узагальнене перетворення Фур'є може розглядатися перетворення Лапласа. Подібним способом можна узагальнити перетворення Фур'є для дискретних за часом систем, і результат такого узагальнення відомий як z-перетворення.

Проектування фільтра за методом sin(x)/x зі зважуванням (Windowed-Sinc).

Імпульсна характеристика ідеального ФНЧ представляється функцією sin(x)/x. Якщо для реалізації цієї частотної характеристики використовувати КІХ-фільтр, то він повинний мати нескінченне число ланок. Метод sin(x)/x зі зважуванням полягає в наступному.

Спочатку відрізають хвости імпульсної характеристики до розумного числа точок (рис. 9.6). Частотна характеристика має занадто великий вплив бічних пелюстків через кінцеві розриви в області кінцевих точок в відсіченій імпульсній характеристиці. Далі застосовують до відсіченої імпульсної характеристики вагову віконну функцію, яка обнуляє кінцеві точки. Обрана вагова віконна функція визначає спад частотної характеристики і бічних пелюстків фільтра. Частотна характеристика фільтра з відсіченою імпульсною характеристикою sin(x)/x має більш плавний перехід від смуги пропускання до смуги затримання та деяку нерівномірність там.

Рис. 9.6. — Проектування КІХ-фільтра за методом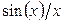
зі зважуванням (Windowed-Sinc).

Проектування КІХ-фільтра за методом рядів Фур'є зі зважуванням.

Метод рядів Фур'є зі зважуванням полягає в початковому математичному визначенні функції передачі H(f) і наступному розкладанні її в ряд Фур'є. Коефіцієнти ряду Фур'є визначають імпульсну характеристику і, отже, коефіцієнти КІХ-фільтра. Потім імпульсна характеристика повинна бути відсічена та піддана зважуванню з використанням віконної функції, як у попередньому випадку. Після відсікання і застосування віконної функції використовується ШПФ для генерації відповідної частотної характеристики. Частотна характеристика може бути змінена вибором віконної функції, хоча точне визначення параметрів такої характеристики в смузі режекції утруднено при будь-якому методі, що використовує зважування з функцією вікна. Порядок виконання операцій.

§ Точне визначення передатної характеристики H(f).

§ Розкладення H(f) у ряд Фур'є: коефіцієнти ряду Фур'є є коефіцієнтами КІХ-фільтра h(k) і його імпульсною характеристикою.

§ Відсікання імпульсної характеристики до N точок.

§ Зважування h(k) з відповідною віконною функцією для згладжування ефекту відсікання.

§ Відсутнє точне керування частотою зрізу; сильна залежність від віконної функції.

Проектування КІХ-фільтра за методом частотної дискретизації.

Цей метод надзвичайно корисний при генерації КІХ-фільтра з довільною частотною характеристикою. H(f) визначається як набір точок амплітудної і фазової характеристик у частотній області. Потім точки перетворюються в дійсні і уявні складові комплексного спектра. Наступним кроком є одержання імпульсної характеристики шляхом узяття комплексного зворотного ШПФ від частотної характеристики. Далі імпульсна характеристика обрізається до N точок і застосовується зважування з функцією вікна для мінімізації ефекту відсікання. Потім результат проектування фільтра повинний бути перевірений шляхом обчислення ШПФ від імпульсної характеристики й оцінки частотної характеристики фільтра. Для одержання бажаної характеристики може знадобитися кілька ітерацій. Порядок виконання операцій такий:

§ визначення H(k) як кінцевого числа спектральних крапок рівномірно розподілених між 0 і 0,5 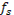(звичайно досить 512);

§ визначення фазових крапок (можна робити рівними 0);

§ перетворення в алгебраїчну форму (дійсна + уявна частини);

§ комплексне зворотне ШПФ масиву H(f) для одержання імпульсної характеристики;

§ відсікання імпульсної характеристики до N точок;

§ зважування h(k) із придатною функцією вікна для згладжування ефектів відсікання;

§ перевірка результату і необхідна корекція;

§ методи САПР більше підходять для ФНЧ, ФВЧ, смугових і режекторних фільтрів.

Проектування КІХ-фільтров з використанням програми Паркса-Маккліллана (Parks-Mаcсlellan).

Метод проектування, заснований на використанні вікон для відсікання імпульсної характеристики й одержання бажаної частотної характеристики, історично був першим методом проектування КІХ-фільтрів. Метод частотної дискретизації популярний у тих випадках, де частотна характеристика є довільною функцією.

Сучасні програми САПР, що істотно спрощують проектування НЧ, ВЧ, смугових і режекторних КІХ-фільтрів. Популярна програма була розроблена Парксом (Parks) і Макклілланом (Mаcсlellan) і використовує алгоритм обміну Ремеза (Remez). Проектування фільтра починається з визначення параметрів: нерівномірності смуги пропускання, нерівномірності смуги затримки (те ж, що ослаблення) і області переходу. У цьому прикладі ми будемо проектувати звуковий НЧ фільтр, що працює при частоті дискретизації 44,1 кГц. Гранична частота смуги пропускання складає 18 кГц. Смуга затримки розпочинається на частоті 21 кГц, нерівномірність смуги пропущення дорівнює 0,01 дБ, а нерівномірність смуги затримки (ослаблення) 96 дБ. Ми також повинні визначити довжину слова (розрядність) коефіцієнтів, що у даному випадку складає 16 розрядів, приймаючи в увагу, що використовується 16-розрядний процесор. Вхідні данні для проектування.

§ Тип фільтра;

§ частота дискретизації — 44 100 Гц;

§ частота смуги пропускання — 18 000 Гц;

§ частота смуги затримки — 21 000 Гц;

§ нерівномірність смуги пропускання — 0,01 дБ;

§ нерівномірність смузі затримки — 96 дБ;

§ довжина слова — 16 біт.

Програма дозволяє нам вибирати між проектуванням, заснованим на зважуванні з використанням віконних функцій, і проектуванням КІХ-фільтрів з фіксованою нерівномірністю Паркса-Маккліллана. Якщо вибрати останній спосіб, то програма оцінює число ланок фільтра, необхідне для його реалізації з дотриманням сформульованих технічних вимог. У даному випадку число ланок дорівнює 69. Можна прийняти це число і продовжити проектування або зменшити число ланок і подивитися, чи можна з меншим числом досягти необхідних характеристик. Вихідні дані програми проектування:

§ Оцінка необхідного порядку фільтра:

¨ Прийняти? Змінити? Прийняти:

§ частотна характеристика (лінійна і логарифмічна шкали);

§ реакція на східчастий вплив;

§ аналіз у S- і Z-площинах;

§ імпульсна реакція: коефіцієнти фільтра (квантування);

§ асемблерний код процесора для КІХ-фільтра.

Приклад проектування.

§ Частота дискретизації 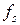=44,1 kSPS.

§ Інтервал дискретизації 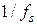=22,7 мкс.

§ Порядок фільтра, N=69.

§ Кількість необхідних команд =N+5=74.

§ Процесорний час на команду =13,3 нс.

§ Загальний час обробки становить 74´13,3 нс=984 нс.

§ Запас часу для інших операцій 22,7 мкс–0,984 мкс =21,7 мкс.

¨ збільшення частоти дискретизації до 1 МГц;

¨ використання більш повільного процесора ЦОС;

¨ збільшення порядку фільтра (до N=1700).