Задачі фільтрація вимірювальної інформації

Нехай на вхід декотрої лінійної системи з передаточною функцією H(p) подається адитивна суміш Z(t) = y(t) + Q(t), де y(t) – корисний сигнал довільної форми, а Q(t) – перешкода (білий шум). До вихідної системи H(p) додамо «бажану» систему H₀(p), котра буде здійснювати потрібне перетворення вхідного сигналу «в ідеалі», тобто при відсутності перешкоди Q. Зрозуміло, що задане перетворення вхідного сигналу системою H(p) буде тривати оптимально, якщо середньоквадратична помилка:

,

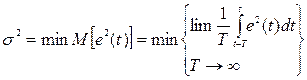де: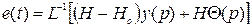

M – знак математичного очікування.

Із виразу для неузгодженості e(t) слідує, що завдання потрібного перетворення корисного сигналу на вході y(t) при наявності перешкоди Q не є тривіальним, тобто не приходить до тотожності H(p)=H₀(p). В той же час це завдання у викладеній вище постановці є достатньо загальною, тому що:

при H₀ = p^k 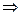H(p)– диференціатор k-го порядку;

при H₀= 1/p 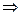H(p) – інтегратор;

при H₀ = e^pT H(p) – прогнозатор (екстраполятор);

при H₀ = 1 = H(p) – фільтр, згладжуючий перешкоду Q.

Отже, схема безперервної фільтрації або згладжування перешкоди Q подана в загальному вигляді на рис. 3.1.

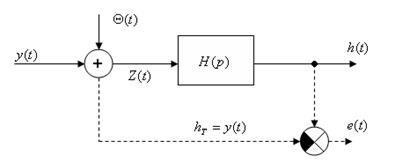
Рис. 3.1. Узагальнена схема безперервного фільтра.

Дійсно, якщо корисний сигнал y(t) є регулярним, то тут, в свою чергу, можливі наступні окремі випадки.

1. Форма корисного сигналу відома: 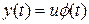, де 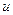– випадкова амплітуда; f(t) – відома функція. Тоді 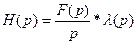і фільтр являє собою послідовне з’єднання узгодженого фільтра F(p)/p (це аналоговий пристрій, на виході котрого співвідношення «сигнал/шум» є максимально можливим) і підсилювача з коефіцієнтом підсилення l(p), залежним від характеристик вхідного сигналу та перешкоди:

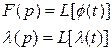
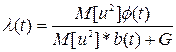
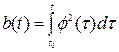
де G – інтенсивність білого шуму Q. При цьому досягається мінімум середньоквадратичної помилки:

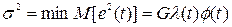(3.28)

Рис. 3.2. Схема оптимальної безперервної фільтрації при відомій формі вхідного сигналу

3. Форма корисного сигналу невідома:

а) завжди можна знайти таку ортогональну систему функцій, що 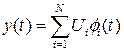, де U_i – випадкова амплітуда, а f_I – відома функція, причому за умовою 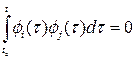, 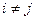. Безумовно, що в цьому випадку оптимальна система фільтрації являє собою паралельне з’єднання узгоджених фільтрів F_i(p)/p на виходах котрих підключені підсилювачі l_i(p).

Мінімум середньоквадратичної помилки складе при цьому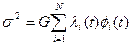

Рис. 3.3. Схема оптимальної фільтрації при невідомій формі сигналу.

б) кожну, заздалегідь невідому, форму сигналу y(t) можна відтворити за допомогою лінійного диференціального рівняння

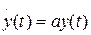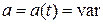; , (3.29)

з початковими умовами в тому числі і при . Насправді, з (3.30) витікає .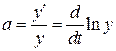

Тоді

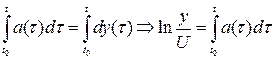
Або

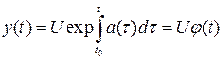; (3.30)

де f(t) = exp 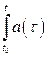dt і, таким чином, в залежності від значення a(t) форма y(t) може бути будь – якою, наприклад:

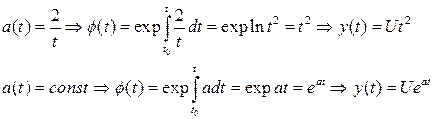
Для формування будь – якої, наперед не заданої, форми f(t) корисного сигналу y(t) необхідний аналоговий пристрій, з алгоритмом функціонування (3.29). Такий пристрій являє собою інтегратор, охоплений позитивним зворотнім зв’язком і на вхід котрого подається нульовий сигнал. На інтеграторі можуть бути встановлені випадкові початкові умови. Тепер, маючи пристрій формування функції f(t), можна скористатися схемою оптимальної фільтрації при відомій формі корисного сигналу y(t). Тоді

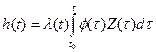(3.31)

Диференціюючи рівняння (4.4) за часом, отримаємо:

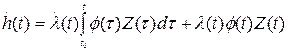(3.32)

Помножимо останнє рівняння на l і віднімемо від нього (3.31), помножене на ¢?l, в результаті маємо:

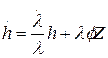(3.33)

Для того, щоб безперервний фільтр, побудований за (3.36), був оптимальним, необхідно функції l і f виразити через мінімум середньоквадратичної помилки s ² та характеристики перешкоди. Це може бути зроблено через (3.28). lf = G/s ². Остаточно:

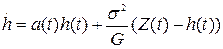(3.34)

Звідки слідує схема оптимального фільтру рис. 3.4.

Рис. 3.4. Оптимальний безперервний фільтр (фільтр Калмана)

Остання схема оптимальної фільтрації складається з формуючого фільтра та попереднього підсилювача з коефіцієнтом підсилення s²(t)/G охоплених негативним зворотнім зв’язком. Цей результат був отриманий Калманом та названий в його честь. Оскільки фільтр Калмана описується диференційним рівнянням, то у дискретному варіанті він повинен мати нескінченну пам’ять. Всі варіанти оптимальної фільтрації, попередні фільтру Калмана, можуть бути отримані з кінцевою пам’яттю Т, для цього достатньо замість інтервалу [t₀; t] розглядати кінцевий інтервал [t-T; t].

3. В задачах збору та обробки вимірювальної інформації корисний сигнал наряду з регулярною частиною має, на відміну від попереднього, і нерегулярну складову Y⁰:

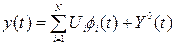, (3.35)

являючи собою випадкову функцію з математичним очікуванням m_Y⁰=0 і котра не може бути уявлена лінійною комбінацією порівняно невеликого числа відомих детермінованих функцій з випадковими коефіцієнтами. Більшості технологічних об’єктів контролю та керування присутня саме нерегулярність корисного сигналу y(t).

Розглянемо оптимальну систему фільтрації і для цього випадку, коли підлегла фільтрації суміш:

.

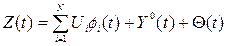є стаціонарною випадковою функцією, а потрібний вихідний сигнал h_T(t) є стаціонарно випадкова функція, стаціонарно пов’язана з Z(t).

Уявимо стаціонарну систему фільтрації, де заради узагальненості Q є адитивна перешкода довільної форми. Тому що синтез оптимальних систем простий для перешкоди у вигляді білого шуму, то зі складу H(p) необхідно виділити складову H_of, котра перетворює нерегулярну вхідну суміш Z(t) з довільною перешкодою в білий шум.

Згідно спектральній теорії стаціонарних випадкових процесів для лінійної стаціонарної системи можна записати:

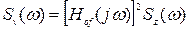, (3.36)

де S z(w), Sv(w) – спектральна щільність відповідних сигналів.

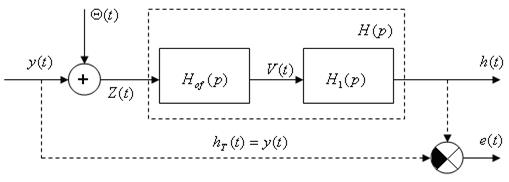
Рис. 3.5. Стаціонарна система фільтрації з відбілюючим фільтром.

Оскільки H_of(jw) є відбілюючий фільтр, то доцільно припустити що K_v(t) = 2ps(t - t) – білий шум з інтенсивністю G = 2p (ідеальний білий шум). Тоді для такого білого шуму S_v (w) = G/2p = 1.

Із (3.36) слідує, що

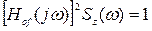, (3.37)

де дійсний вираз S_z(v) завжди можна уявити в вигляді добутку спряжених нелінійних виразів:

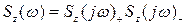(3.38)

Останні дві рівності дають:

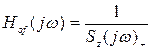(3.39)

Зробивши зворотній перехід jw = p отримаємо:

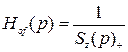, (3.40)

де S_x(p)₊ - має нулі в лівій напівплощині змінної p або в верхній напівплощині змінної w. Це значить, що відбілюючий фільтр з передаточною функцією (3.40) (або частотною характеристикою (3.38) найбільш просто реалізується та стійкий.

Відомо, що система фільтрації стає оптимальною за точністю, якщо частотна характеристика системи:

. (3.41)

задовольняє інтегральному рівнянню Вінера – Хопфа, котре для розгляданої стаціонарної системи з нескінченною пам’яттю має вигляд:

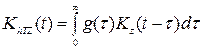, (3.42)

де g(t)=F^-1[H(jw)] – шукана вагова функція оптимальної за точністю системи фільтрації з неперервною областю спостереження. Система, вагова функція котрої задовольняє (3.42), називається безперервним фільтром Вінера з нескінченною пам’яттю.

Запишемо рівняння (3.42) в Фур’є – виразах:

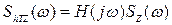. (3.43)

або з врахуванням (3.44)

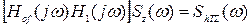. (3.44)

Підставимо в (3.44) рівняння (3.38) і виконаємо факторизацію (3.38)

.

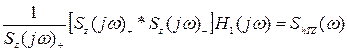Вирішимо відносно невідомої :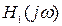

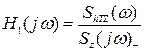, (3.45)

S_hTZ(w) є дрібно – раціональною функцією, тому і (3.45) має той же вигляд, його можна розкласти на суму елементарних дріб.

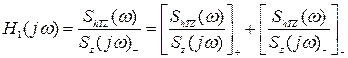(3.46)

Лівий доданок вміщає суму елементарних дріб, у котрій всі полюси у верхній напівплощині змінної w, а другий містить всі дроби з полюсами в нижній напівплощині. Операція сепарації дозволяє виділити з (3.45) реалізуєму (стійку) частину:

.

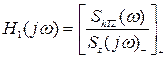Тоді шукана частотна характеристика безперервного фільтра Вінера:

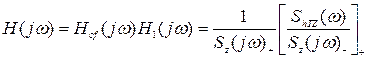(3.47)

Алгоритм (3.47) носить універсальний характер, тому що вид задачі в ньому локалізований для S_hTL(w) між фактичним сигналом вході Z(t) та ідеальним сигналом на виході h_T(t). Для розглянутої задачі оптимальної фільтрації вимірювальної інформації коли h_T(t)=y(t) і при наявності адитивної перешкоди: S_x(w)=S_y(w)+S_Q(w), взаємна спектральна щільність має вигляд:

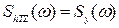. (3.48)

Шукані характеристичні функції фільтра Вінера набувають реалізуємих обрисів:

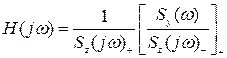
або при jw = p :

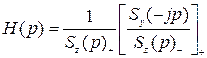. (3.49)

При цьому мінімальна середньоквадратична похибка буде:

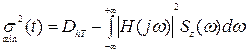. (3.50)

Працездатність системи з рис. 3.6 можна підвищити, якщо в ній буде негативний зворотній зв’язок. Тоді отримаємо замкнутий фільтр Вінера, де:

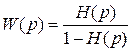, (3.51)

а H(p) визначена у (3.51).

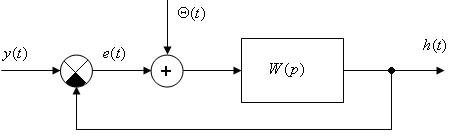
Рис. 3.6. Безперервний фільтр Вінера з негативним зворотнім зв’язком.

Коли Q – білий шум, то схему рис. 3.6 називають канонічною. Теоретично вирішена вище задача є окремим випадком загальної задачі оптимального перетворення сигналу автоматичною системою. Більш вузька задача – фільтрація вимірювальної інформації, де вихідний сигнал датчика є стаціонарним випадковим; вирішується теорією стаціонарних випадкових процесів. Ось чому фільтри Вінера називають статистичними. Якщо інтеграл Вінера – Хонфа невласний, то область спостережень має розмір [- ∞; + ∞].

Такий нереальний фільтр корисний для отримання асимптотичної оцінки фільтрації і порівняння похибки згладжування в реальних фільтрах. Фільтр Вінера (3.49) реалізується, коли розміри області спостереження

[t-T; T], де T – об’єм пам’яті цього статистичного фільтра. Але точність оцінки сигналу та перешкоди дуже наближена. Тоді задачу фільтрації вирішують для найбільш поширеного вузького набору статистичних характеристик.

Представимо структуру електронної системи в такому виді:

Рис. 3.7. Структурна схема електронної системи.

Контрольні запитання

1.Що представляє собою перешкода (білий шум). В чому її відмідність від інших перешкод?

2.Яку перешкоду називають адитивною?

3.Які бувають завади? Обгругтувати їх відмінність один від одного.

4.В яких межах лежить ступінь регулярності сигналів промислових систем керування у реальних виробничих умовах?

5.В чому полягає сенс виконання операцій факторизації та сепарації?

6.Навіщо використовують перетворення Лапласа вхідного сумарного і вихідного сигналів?

7.Розповісти принцип фільтрації Вінера і Калмана.

8.Як перейти від параметру р до параметру w ?

9.Яке фізичне значення мають полюси функцій?

10.В чому особливість фільтрації вимірювальної інформації?

11.Навести схему фільтрації з відбілюючим фільтром.

12.Записати рівняння частотної характеристики безперервного фільтру Вінера.

13.Обґрунтуйте чому фільтри Вінера називають статистичними. Як змінюється схема безперервної фільтрації або згладжування перешкоди при різних значеннях вхідного сигналу?