Граничні помилки не реалізованих електронних систем
Зі зменшенням швидкості протікання технологічних процесів збільшується значення початкової ординати та величина максимуму функції спектральної щільності. Чим нижче швидкість, тим менше параметр затухання автокореляційної функції. Площа під кривою спектральної щільності дорівнює дисперсії центрованого процесу, тому з збільшенням швидкості процесу функція спектральної щільності буде притискатися до осі частот, стаючи одночасно більш пологою. Така поведінка функції спектральної щільності дозволяє ввести поняття білого шуму, тобто випадкової функції з постійною спектральною щільністю, що дуже часто зустрічається в додатках. Коли збільшується параметр затухання, кореляційна функція стає пікоподібною, відрізняючись від нуля тільки в дуже вузькій області поблизу нуля. Одночасно кривизна функції спектральної щільності при малих частотах буде зменшуватись і, в кінці кінців, в дуже широкій області значень частоти можна вважать спектральну щільність постійною. Тому функцію, яка має достатньо великий параметр затухання, можна вважати функцією з постійною спектральною щільністю n=2В/ц. Ординати білого шуму, узяті для будь-яких різних моментів часу. являються некорельованими випадковими величинами. Один і той же процес в одній задачі можна вважати білим шумом, а в іншій доводиться враховувати залежність спектральної щільності від частоти. Наприклад, неконтрольовані збурення, які визначаються на основі кореляційного або когерентного аналізу, доцільно вважати білим шумом. Порядок апроксимуючого поліному перешкод звичайно невисокий, що витікає з фізичного смислу цього поняття, яке характеризується деякою невизначенністю. У випадку повної визначеності такого сигналу його слід би віднести до корисного.
Коли спектральна щільність перешкод апроксимована білим шумом, сума сигналу з однією періодичною складовою та перешкоди має вигляд:
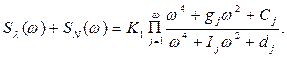 (2.1)
(2.1)
Sl(w), SN(w) – спектральні щільності корисного сигналу та перешкод;
Sx(w) – спектральна щільність суми корисного сигналу і перешкоди.
Поліноми чисельника та знаменника мають однаковий порядок. Дослідження випадкових процесів, які протікають в розглянутих об'єктах автоматизації, показало, що w=1 і граничний порядок поліномів не перевищує чотирьох.
Нижній рівень систем автоматичного керування характеризується відносно високим рівнем перешкод, тому вимоги до структури та параметрів перешкодостійких систем суперечні. Наприклад. в системі прокатна кліть - деформований метал для придушення впливу збурень модуль жорсткості кліті повинен бути якомога більше, а для зменшення впливу ексцентриситету як можна менше.
Аналогічна ситуація виникла при визначенні коефіцієнта передачі між збуренням та керуванням. Недокомпенсація впливу збурень, як і перекомпенсація ведуть до збільшення відносного середньоквадратичного відхилення.
Найбільш поширеним критерієм оптимізації являється мінімум середньої квадратичної помилки.
Дисперсія помилки системи, до якої не ставиться вимога фізичної реалізуємості, не перевищує дисперсію помилки фільтрації. отриману при використанні фізично реалізуємої системи керування. Величина мінімальної помилки, знайдена для нереалізуємої системи, може служити оцінкою знизу для дисперсії помилки у фізично реалізуємій. Обчислення такої оцінки корисне для характеристики граничних можливостей зменшення помилки фільтрації та оцінки відношення дисперсій сигналу та перешкоди в смузі сигналу.
Дисперсія помилки фізично нереалізуємої системи перетворення сигналу:
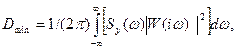 (2.2)
(2.2)
Sy(w) – спектральна щільність сигналу на виході;
W(iw) – частотна характеристика фільтру;
Сумарна дисперсія вихідного сигналу:
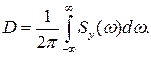 (2.3)
(2.3)
Розділивши вираз (2.2) на (2.3), одержимо відносну помилку відтворення у вигляді:
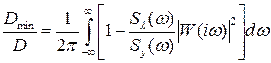 (2.4)
(2.4)
Dmin – залишкова дисперсія прогнозу;
Частотна характеристика оптимальної динамічної системи дорівнює (2.2), а функція Sl(w) є функцією дійсної змінної, тому:
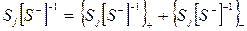 . (2.5)
. (2.5)
Тоді:
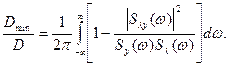 (2.6)
(2.6)
Оскільки другий член під інтегрального виразу (2.6) представляє собою функцію когерентності, то:
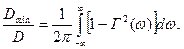 (2.7)
(2.7)
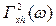 – функція множинної когерентності контрольованих збурень на товщину.
– функція множинної когерентності контрольованих збурень на товщину.
В тому випадку, коли когерентність на всіх частотах дорівнює одиниці, функція У(t) має при лінійному перетворенні функції l(t) нульову середньоквадратичну помилку, тобто рівень перешкод в цьому випадку нульовий. Зі збільшенням рівня перешкод функція когерентності стає менше одиниці і дисперсія помилки відрізняється від нуля. Якщо функція когерентності дорівнює нулю, то відношення дисперсій дорівнює одиниці.
Функція множинної когерентності запишеться у вигляді:
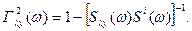 (2.8)
(2.8)
Поповнена матриця розмірності (h+1 )(h+1) має вигляд:
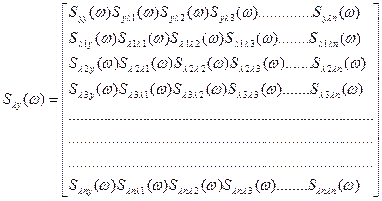 (2.9)
(2.9)
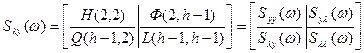 ,
,
Si (w)– і-й елемент головної діагоналі 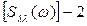 .
.
Функція частинної когерентності при виключенні впливу інших вхідних параметрів:
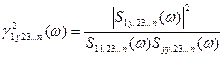 . (2.10)
. (2.10)
Залишкова спектральна матриця:
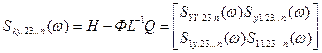 .
.
Матриці H, Ф, Q, L знаходяться з поповненої матриці 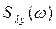 . В окремому випадку, якщо h=1, функція парної когерентності має вигляд:
. В окремому випадку, якщо h=1, функція парної когерентності має вигляд:
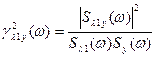 . (2.11)
. (2.11)
 – функція парної когерентності вхідного параметру на вихідний.
– функція парної когерентності вхідного параметру на вихідний.
При графічному методі розрахунку залишкової спектральної щільності вихідного розміру за відомою функцією когерентності та спектральної щільності нерегульованого розміру залишкова дисперсія у статиці визначається за рівнянням:
Dmin/D=1-R2 . (2.12)
В задачі статистичного синтезу із суми контрольованого та неконтрольованого вхідних сигналів необхідно відтворити перший сигнал з мінімальною середньоквадратичною помилкою в сталому режимі. В тому випадку, якщо оператор бажаного відтворення одиничний, то взаємна спектральна щільність вхідного та вихідного процесів дорівнює спектральній щільності корисного сигналу у відповідності з відомою теоремою Вінера - Хінчіна. З врахуванням некорельованості корисного сигналу та перешкод отримаємо частотну характеристику:
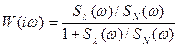 . (2.13)
. (2.13)
Оптимальний нереалізуємий фільтр має коефіцієнт передачі. який змінюється від одиниці до нуля в залежності від відношення спектральних щільностей корисного сигналу та перешкод, В цьому випадку відносна помилка дорівнює:
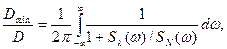 (2.14)
(2.14)
що співпадає з виразом для мінімальної помилки, так як в цьому випадку:
 (2.15)
(2.15)
Гранична похибка фільтрації тим менше, чим менше перекриваються спектри корисного сигналу та перешкод. Якщо спектри не перекриваються, то помилка може бути рівною нулю.
Mожна отримати:
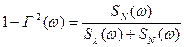 . (2.16)
. (2.16)
Тоді взаємозв'язок між відносним рівнем перешкод та функцією когерентності має вигляд:
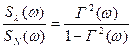 . (2.17)
. (2.17)
Якщо когерентність на всіх частотах дорівнює одиниці, то перешкоди дорівнюють нулю і відношення дорівнює нескінченності. Якщо когерентність на всіх частотах дорівнює нулю, то і указане відношення буде нульовим. Інтегрування дозволяє отримати величини дисперсій:
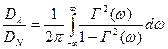 . (2.18)
. (2.18)
Якщо замінити функції Г2(w) їх середніми значеннями, то:
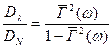 . (2.19)
. (2.19)
Результати розрахунків відношення дисперсій для квадратного кореня значень когерентності можуть бути представлені в вигляді таблиці 2.4.
З врахуванням виразу (2.15) функція парної когерентності дорівнює:
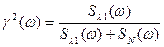 . (2.20)
. (2.20)
Формули для аналітичного розрахунку функції парної когерентності представлені на основі поширених апроксимацій спектральних щільностей корисного сигналу та перешкод.
Таблиця 2.4. Значення відношень корисного сигналу і перешкод та квадратного кореня з середньоінтегральних значень функції когерентності
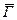
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 |
| a | 0,0 | 0,01 | 0,052 | 0,099 | 0,19 | 0,33 | 0,562 | 0,961 |
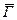
| 0,75 | 0,8 | 0,85 | 0,9 | 0,935 | 0,95 | 0,975 | - |
| a | 1,286 | 1,78 | 2,60 | 4,26 | 5,93 | 9,26 | 19,25 | - |
Якщо відсутні аналітичні моделі спектральних щільностей, розрахунки виконують на основі експериментальних даних. З врахуванням рекомендацій авторами розроблена методика розрахунку функцій когерентності з використанням ПК. Методика дозволяє здійснити розрахунок функцій множинної, парної та частинної когерентності, амплітудні та фазові характеристики динамічних систем.
Відношення дисперсій корисного сигналу та перешкоди в смузі корисного сигналу:
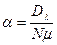 . (2.21)
. (2.21)
Залишкова дисперсія еквівалентна добутку спектральної щільності перешкод на параметр затухання кореляційної функції. Тоді:
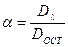 . (2.22)
. (2.22)
З врахуванням того, що Dy=Dl+Dост, маємо:
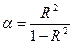 . (2.23)
. (2.23)
На основі функцій когерентності відношення спектральних щільностей корисного сигналу та перешкоди дорівнює:
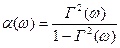 . (2.24)
. (2.24)
Інтегрування дозволяє знайти середнє значення указаного коефіцієнта:
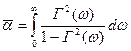 . (2.25)
. (2.25)
Це значення коефіцієнта 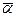 дещо завищене, оскільки не враховуються умови фізичної реалізації рішення, що збільшує втрати та зменшує коефіцієнт a.
дещо завищене, оскільки не враховуються умови фізичної реалізації рішення, що збільшує втрати та зменшує коефіцієнт a.
Відношення спектральних щільностей:
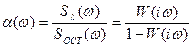 . (2.26)
. (2.26)
Інтегрування дозволяє отримати середнє значення:
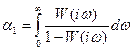 .
.
При розрахунках потрібно враховувати модуль комплексних чисел, тобто:
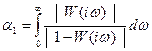 .
.
Отримане значення менше, тобто a1<a, тому при розрахунку нових значень параметрів передаточної функції модуль чисельника збільшиться в меншому ступені, ніж знаменника. Додатковий рівень із-за помилок вимірювання можна визначити за паспортними даними датчика, тоді спектральна щільність корисного сигналу:
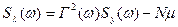 .
.
Відношення спектральних щільностей:
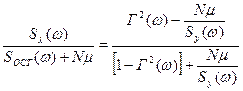 . (2.27)
. (2.27)
Середнє значення відношення дисперсій корисного сигналу та перешкоди:
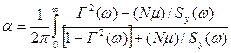 . (2.28)
. (2.28)
Аналогічно в сталому режимі для випадкових величин:
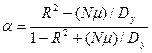 . (2.29)
. (2.29)
Наприклад, при R = 0,7, коли N = 0, a=1; при (Nm) Dy=0,02 a=0,82.
Контрольні запитання
1.Навести приклад випадкового процесу.
2.Що показує функція середнього квадратичного відхилення 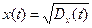 .
.
3.Який процес називається стаціонарним і нестаціонарним.
4.Що показує параметр a та a1?
5.Що являють собою детерміновані і стохастичні сигнали?
6.Для чого необхідна операція фільтрації вихідних сигналів?
7.Що характеризує параметр затухання?
8.Назвіть математичну модель яку використовують для описання широкого класу явищ.
9.Чи є обмеження у потужності білого шуму?
10.Що таке фізично нереалізуєма система?
11.Чи доцільно використання спеціальної фільтруючої програми - так званого дискретного фільтра?
12.Як змінюється коефіцієнт передачі нереалізованого фільтру в залежності від відношення спектральних щільностей корисного сигналу і перешкоди ?
13.Яку функцію можна вважати функцією з постійною спектральною щільністю?
14.Для чого використовують поповнену матрицю Sly(w).
15.Наведіть формулу відношення дисперсій корисного сигналу та перешкоди в смузі корисного сигналу?
Дата добавления: 2015-06-27; просмотров: 964;
