Структурний та параметричний синтез

На входи підсистем керування технологічними процесами різних ієрархічних рівнів надходять корисні сигнали, які потрібно перетворити за заздалегідь заданим алгоритмом. Відомі алгоритми: відтворення, масштабувания, інтегрування, диференціювання, запізнення і упередження. Для більш точного відтворення корисного сигналу потрібна якнайвища швидкодія автоматичної електронної системи. Однак у природі завжди існують перешкоди, що спотворюють вхідний сигнал. Їхня природа різноманітна і може визначатися обмеженими ресурсами системи керування, обмеженнями керування, неточністю виміру параметрів, кінцевою точністю елементної бази, з якої створюються системи керування, неадекватністю алгоритмів перетворення сигналів і т.ін. Тому перед системою керування також стоїть інша задача: не пропустити на вихід перешкоди. Для цього швидкодія системи керування повинна бути якнайнижчою. Зовсім не пропускає перешкоду система керування з нульовою швидкодією. Тому в промислових умовах завжди виникає суперечлива задача вибору оптимальної швидкодії за принципом «КВАПСЯ ПОВІЛЬНО».

Розділяють дві принципово різні задачі структурного і параметричного синтезу оптимальної системи. Рішення задачі структурного синтезу більш переважне, але значно складніше, ніж рішення другої - задачі параметричного синтезу. У першому випадку знаходиться оптимальна за обраним критерієм структура системи, що забезпечує виконання заданого нами алгоритму перетворення, а потім обчислюються параметри такої системи. Стала помилка такої системи, що складається з двох складових – від неповного відтворення сигналу і відтворення перешкоди - найменша, тобто при певних обмеженнях не можна побудувати кращу систему керування для заданого класу алгоритмів перетворення, систем керування, обраного критерію оптимальності і вхідних сигналів. Системи поділяються на два класи: лінійні і нелінійні системи керування. Як критерій найбільше часто застосовують – мінімум середньої квадратичної помилки – через його простоту. Вхідний стохастичний сигнал розглядається як стаціонарний і ергодичний. Тому оптимальна система за критерієм мінімуму середнього квадрата шукається в класі лінійних систем для відтворення стаціонарного ергодичного сигналу зашумленного перешкодою у вигляді білого шуму. Така перешкода являє собою дельта імпульс, свого роду миттєвий спалах, амплітуда якого миттєво змінюється від нескінченності до нуля, є деякою ідеалізацією реально діючих перешкод.

У задачах параметричного синтезу структура системи керування існує за певною умовою. Через можливу структурну неоптимальність системи керування стала помилка більше, ніж у випадку оптимальної структури системи. Рішення задачі включає складання функціоналу помилки системи керування і знаходження його мінімуму. Значення параметра контуру регулювання, що доставляє мінімум функціоналу, вважається оптимальним.

Допущення стаціонарності й ергодичності вхідного сигналу дозволяє використовувати добре розроблений математичний апарат регресійного та кореляційного аналізів і значно скоротити обсяг необхідних обчислень. Для розрахунку досить використовувати найпростіші апроксимації автокореляційних функцій із загасаючою однією періодичною складовою, коли поліном спектральної щільності сигналу дорівнює чотирьом. Це мінімальний порядок полінома, яким описується випадковий сигнал з однією періодичною складовою (одна резонансна частота коливань сигналу). Коли періодична складова відсутня, то тоді порядок полінома дорівнює двом. Такі приклади досить повно описані в технічній літературі. Більш складний сигнал можна розглядати як комбінацію поліномів четвертого і другого ступенів.

Сигнали на входах систем керування являють собою суму корисного сигналу і перешкоди. Сигнали, що надходять на входи систем керування, описуються автокореляційними функціями, що апроксимовані аналітичними функціями, поліноми спектральних щільностей яких мають парний порядок: другий, четвертий і т.д.

Важливою характеристикою випадкового сигналу з періодичною складовою є ступінь регулярності, що визначається відношенням резонансної гармонійної складової до параметра загасання автокореляційної функції. При великому значенні ступеня регулярності ординати сигналу виявляються сильно корельованими і реалізація процесу стає схожою на гармонійний сигнал, наближаючись до детермінованого при відсутності перешкоди. Такі сигнали докладно розглянуті в класичній теорії автоматичного регулювання. При невеликому значенні ступеня регулярності періодичність на резонансній частоті стає мало значимою і сигнал наближається до стохастичного без періодичної складової. Такі прості сигнали докладно описані в теорії випадкових процесів. У реальних виробничих умовах ступінь регулярності сигналів промислових систем керування знаходиться в межах від нуля до нескінченості. Передавальна функція фізично нереалізуємої системи управління дорівнює відношенню двох поліномів

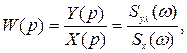(3.1)

де 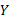(p), X(p) – зображення по Лапласу вхідного сумарного і вихідного сигналів;

S_yl(p) – взаємна спектральна щільність корисного і вихідного сигналів;

S_X(p) – спектральна щільність вхідного сигналу.

Для задачі відтворення корисного сигналу на фоні адитивної перешкоди відповідно до теореми Вінера-Хінчина можна записати

S_yl(p) = S_l(p).

Фізична реалізація вимагає відкидання нестійких рішень, які обумовлені коренями (полюсами) нижньої півплощини параметру частоти. Знаходження нулів не принципове, оскільки нулі нижньої півплощини можуть вплинути лише на не мінімальну фазовість системи але не на показники стійкості.

Отримання фізично реалізуємої оптимальної за критерієм мінімуму середньоквадратичної помилки структури керованої системи припускає виконання з функцією (3.1) ще двох операцій: факторизації спектральної щільності зашумленного вхідного сигналу і сепарації відношення спектральної щільності корисного сигналу і факторизованої спектральної щільності з коріннями в правій напівплощині параметра p. В цьому випадку рівняння Вінера має вигляд

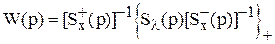, (3.2)

де S_x(p)=S_x⁺(p)S_x^–(p) – факторизація спектральної щільності вхідного сигналу;

{S_l(p)[S_x^–(p)]^-1}₊ – операція сепарації.