Стохастичний синтез форсованих систем другого порядку

Розглянемо суму спектральної щільності випадкового сигналу з періодичною складовою та перешкоди – білого шуму. Поширені дві апроксимації спектральної щільності корисного сигналу – диференцьованою і недиференцьованою функціями.

Для першої апроксимації маємо:

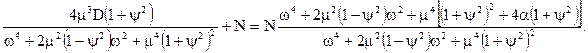
Оскільки для спектральної щільності сигналу використовується відношення резонансної частоти до параметру затухання як ступінь регулярності сигналу, то логічно ввести аналогічну характеристику для полінома чисельника сумарного сигналу. Дрібно-раціональна функція має вигляд:

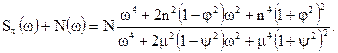(4.18)

Невідомі параметри знайдемо із системи рівнянь:

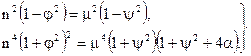
Рішення системи рівнянь можна представити в тригонометричній і алгебраїчній формах. В тригонометричній формі невідомі параметри – параметр затухання і ступінь регулярності полінома чисельника сумарного сигналу дорівнюють:

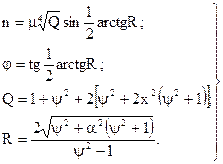(4.19)

В алгебраїчній формі вони дорівнюють:

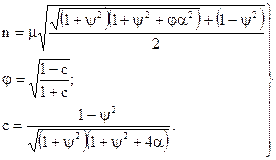(4.20)

Легко показати, що одержані - алгебраїчна та тригонометрична форми запису є еквівалентні.

Якщо рівень перешкоди дуже малий, то ступінь регулярності наближається до одиниці. Коли рівень перешкоди дуже великий, тоді параметр затухання сумарного сигналу співпадає з параметром затухання сигналу, як і резонансні частоти, а ступінь регулярності чисельника сумарного сигналу дорівнює ступіню регулярності корисного сигналу.

Таким чином, при малому рівні перешкоди ступінь регулярності чисельника сумарного сигналу не залежить від ступіня регулярності корисного сигналу і відношення середньоквадратичних відхилень сигналу і перешкоди і близьке до одиниці. З підвищенням рівня перешкоди ступінь регулярності чисельника сумарного сигналу наближається до ступеня регулярності корисного.

Якщо корисний сигнал з періодичною складовою апроксимовано більш простою недиференцьованою функцією, тоді сумарний сигнал має вигляд:

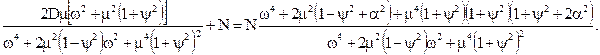
Невідомі параметри знайдемо із системи рівнянь:

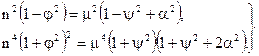
Звідки знайшли параметри сумарного сигналу. Параметр затухання:

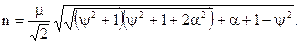(4.21)

Ступінь регулярності дорівнює:

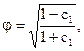(4.22)

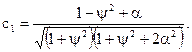
Для великого рівня перешкоди залежності ступенів регулярності корисного сигналу і чисельника сумарно одинакові для недиференційної і диференційної апроксимацій сигналу. Але для малого рівня перешкоди для недиференційної апроксимації сигналу ступінь регулярності чисельника сумарного сигналу дорівнює 0,408 для нульового рівня ступеня регулярності сигналу і відповідно одиниці для рівня сигналу, рівного безкінечності. Вказані криві мають спільну точку, коли ступіні регулярності однакові для недиференційної апроксимації і дорівнюють 0,46, а для диференційної апроксимації відповідно одиниці. Для других відношень середньоквадратичних відхилень сигналу і перешкоди криві знаходяться в заштрихованих секторах з тими же точками однакового рівня ступіней регулярності.

Оскільки вхідний сигнал може бути добутком більш простих, розглянемо найбільш поширені випадки.

При переході від змінної р до змінної ω ліва та права напівплощини переходять відповідно в верхню та нижню напівплощини комплексної площини ω. Дійсно, в наслідок зміни р на іω, одержали:

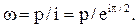(4.23)

При переході від якої-небудь точки площини р до відповідної точки площини ω треба повернути радіус-вектор, проведений в площині р, до цієї точки на 90˚ по годиниковій стрільці.

Наприклад, спектральна щільність сумарного корисного диференцьованого випадкового сигналу і перешкоди має вигляд:

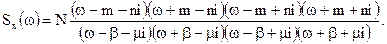(4.24)