Методика Ван-Трiса.

Виконаємо операцiю факторизацiї, коли комплексно спряженi функцiї, всi нулi та полюси яких знаходяться вiдповiдно в верхнiй та нижнiй напiвплощинах параметра частоти, дорiвнюють:

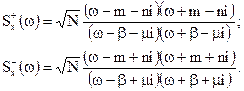
Оптимальна передаточна функцiя дорiвнює:

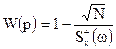
Пiсля перетворень одержали передатну функцію форсованої ланки другого порядку:

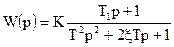, (4.27)

дe K – коефiцiєнт передачi;

Т,Т₁– постiйнi часу;

ξ – вiдносний коефiцiєнт затухання.

Постiйна часу знаменника дорiвнює:

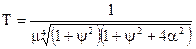, (4.28)

де μ – параметр затухання корисного сигналу;

ψ – cтупiнь регулярностi корисного сигналу;

α – вiдношення середньоквадратичних вiдхилень сигналу i перешкоди.

Чим бiльше ступiнь регулярностi корисного сигналу, тим менше згаданий добуток, що тим сильнiше, чим бiльше вiдношення параметрiв сигналу i перешкоди.

Вiдносний коефiцiєнт затухання:

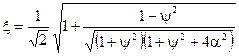. (4.29)

Для дуже малого вiдносного рiвня перешкоди вiдносний коефiцiєнт затухання не залежить вiд ступеня регулярностi корисного сигналу i наближається до постiйного значення 0,707. Для дуже великого рiвня перешкоди формула для оцiнки добутку постiйної часу на параметр затухання спiвпадає з вiдносним коефiцiєнтом затухання:

.

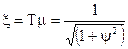Вiдносний коефiцiєнт затухання завжди менше одиницi, для одиничного ступеня регулярностi корисного сигналу дорiвнює 0,707 незалежно вiд корисного сигналу i перешкоди. Для ступеня регулярностi в межах вiд нуля до одиницi вiдносний коефiцiєнт затухання знаходиться в межах вiд 0,707 до одиницi.

Коефiцiєнт передачi системи дорiвнює:

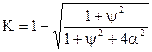. (4.30)

Чим бiльше ступiнь регулярностi корисного сигналу, тим менше значення коефiцiєнту передачi. Для дуже малого рiвня перешкоди коефiцiєнт передачi дорiвнює одиницi i не залежить вiд ступеня регулярностi. При дуже великому рiвнi перешкоди коефiцiєнт передачi зменшується до нуля.

Постiйна часу форсування:

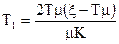. (4.31)

Добуток постiйної часу на параметр затухання корисного сигналу зменшується з ростом ступеня регулярностi i збiльшенням рiвня перешкоди. Коли вiдносний рiвень перешкоди дуже малий, указаний добуток не залежить вiд ступеня регулярностi i дорiвнює 0,5.

Для поширених в техніці спектральних щiльностей корисних сигналів без періодичної складової та з періодичною складовою, яка описується диференційною і недиференційною функціями, а також більш складних моделей та перешкоди в виді білого шуму виконали оптимальний синтез перешкодостійких систем. Повні і неповні поліноми характеристичних рівнянь сигналу мають порядок два, чотири, шість, що відповідає такій же кількості полюсів, причому в двох останніх випадках можуть включати дві пари комплексно-спряжених, характеризуючих коливальні процеси.