Структурний синтез систем довільного порядку.
При відсутності кореляції корисного сигналу і адитивної перешкоди спектральна щільність сумарного вхідного сигналу:, де  – спектральна щільність завади.
– спектральна щільність завади.
Розглянемо найбільш простий випадок, коли корисний сигнал мало змінюється, а перешкода являє собою дельта-імпульс, тоді спектральні щільності сигналу описуються швидко спадаючими гіперболічними функціями заданого порядку а завада постійним рівнем сигналу :
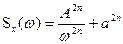 . (4.37)
. (4.37)
Фізична реалізація оптимальної за критерієм мінімуму середньоквадратичної помилки структури системи включає дві додаткові операції - факторизації спектральної щільності вхідного сигналу з шумовою складовою і сепарації відносини спектральних щільностей корисного сигналу і факторизованої спектральної щільності з коренями в правій (нестійкій) півплощині параметра p. Остання операція за рахунок відкидання нестійких складових руху завжди підвищує усталену похибку системи. За рахунок оптимальності перетворення таке підвищення похибки мінімальне.
Для виконання операції факторизації необхідно знайти корені поліномів спектральної щільності зашумленого сигналу і розкласти поліном на добуток простих множників, що відповідають лівій (стійкій) півплощині і правій (хитливій) півплощині параметру p. Математичну операцію сепарації виконати складніше. Існує два основних прийоми: розкладання дрібно-раціональної функції відносини спектральних щільностей на суму простих множників та шляхом зворотного перетворення Лапласа з застосуванням теореми Коші про відрахування і пряме перетворення Лапласа сепарованого шляхом інтегрування вираження в півплощині стійких рішень. Для інженерних розрахунків можна використовувати спрощене рішення Ван-Тріса, яке доведене для умов, коли перешкода представлена білим шумом і корені характеристичного поліному відносини спектральних щільностей дійсні.
Приклад. Розглянемо структурний синтез системи керування для випадку 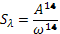 . Спектральна щільність сумарного (шумового) вхідного сигналу:
. Спектральна щільність сумарного (шумового) вхідного сигналу:
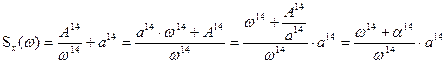 , (4.38)
, (4.38)
де 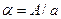
Розкладемо поліном чисельника на прості співмножники, коли 7 коренів розташовані у верхній півплощині
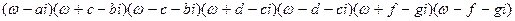 (4.39)
(4.39)
і 7 коренів у нижній півплощині
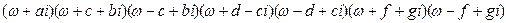 (4.40)
(4.40)
Таким чином, задача зводиться до знаходження коренів рівняння 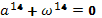 (тобто чисел a, b, c, d, e, f, g). Вирішуючи цю задачу в середовищі математичних обчислень MATHCAD 2000 PROFESSIONAL /1/ (поставивши курсор у поле рівняння
(тобто чисел a, b, c, d, e, f, g). Вирішуючи цю задачу в середовищі математичних обчислень MATHCAD 2000 PROFESSIONAL /1/ (поставивши курсор у поле рівняння 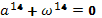 поруч з «
поруч з « 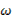 » і вибравши пункт меню Символіка | Перемінні | Дозволити), одержуємо наступні корені:
» і вибравши пункт меню Символіка | Перемінні | Дозволити), одержуємо наступні корені:
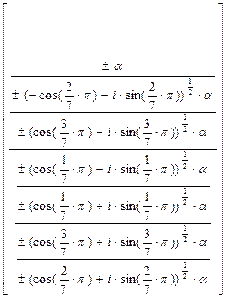
| або в числовому вигляді: 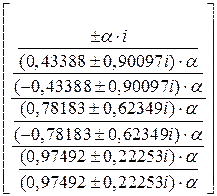
|
Корені з негативною уявною частиною відкидаємо. Тоді порівнюючи (4.40) і (4.39), знаходимо: 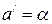 ;
; 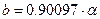 ;
; 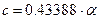 ;
; 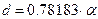 ;
; 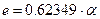 ;
; 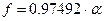 ;
; 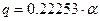 .
.
Таким чином, факторизація спектральної щільності вхідного сигналу дає:
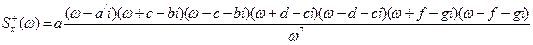 (4.41)
(4.41)
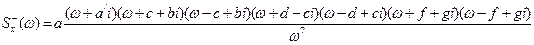 (4.42)
(4.42)
Перейдемо до перемінного p = i 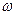 , помноживши (4.41) на i7/i7:
, помноживши (4.41) на i7/i7:
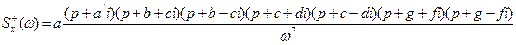 (4.43)
(4.43)
Підставляємо замість a-g їхні числові значення, і, провівши спрощення, одержуємо:
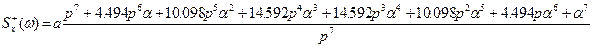
Таким чином, передатна функція замкнутої системи має такий вигляд:
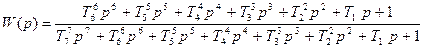 ,
,
де 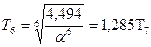 ;
; 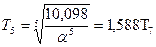 ;
; 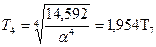 ;
;
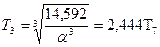 ;
; 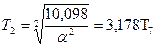 ;
; 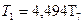 ;
; 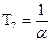 .
.
Результати розрахунків проведених у відповідності вищеописаним алгоритмом для спектральних щільностей корисного сигналу 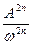 , де n=1,2,3,4,5,6,9 і 11 та відносного рівня завади
, де n=1,2,3,4,5,6,9 і 11 та відносного рівня завади 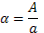 наведені в таблиці 4.1:
наведені в таблиці 4.1:
Таблиця 4.1. Оптимальні за критерієм СКО структури систем
| № | Замкнутої системи | Розімкнутої системи | Параметри |
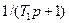
| 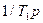
| T1=1/ 
| |
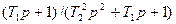
| 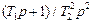
| T2=1/  T1= T1= 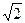 / / 
| |
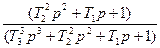
| 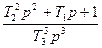
| T3=1/  T2= T2= 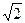 / /  T1=2/ T1=2/ 
| |
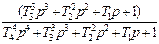
|
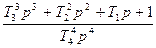
| T4=1/  T3=1.337/ T3=1.337/  T2=1.736/ T2=1.736/  T1=3.613/ T1=3.613/ 
| |
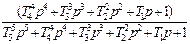
|
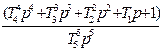
| T5=1/  T4=1.341/ T4=1.341/  T3=1.736/ T3=1.736/  T2=3.288/ T2=3.288/  T1=3.236/ T1=3.236/ 
| |
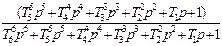
|
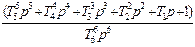
| T6=1/  T5=1.310/ T5=1.310/  T4=1.653/ T4=1.653/  T3=3.091/ T3=3.091/  T2=3.732/ T2=3.732/  T1=3.864/ T1=3.864/ 
| |
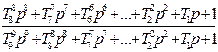
|
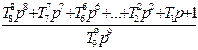
| T9=1/  T8=1.261/ T8=1.261/  T7=1.529/ T7=1.529/  T6=1.834/ T6=1.834/  T5=3.205/ T5=3.205/  T4=3.687/ T4=3.687/  T3=3.364/ T3=3.364/  T2=4.421/ T2=4.421/  T1=6.374/ T1=6.374/ 
|
Дата добавления: 2015-06-27; просмотров: 646;
