Структурна фільтрація рожевої завади

Дана спектральна густина сигналу:

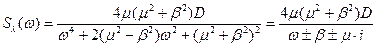
Приймемо дисперсію D рівної 1. Перешкода представлена у вигляді кольорового шуму, а точніше його спектральної густини:

.

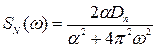Ця спектральна густина описується процесом Орнштейна-Уленбека (1930), який є реалізацією корельованих випадкових блукань. Він має на увазі, що частинка, що має велику швидкість, має велику вірогідність зіткнутися, т.ч. всі частинки мають властивість повертатися до нульової швидкості і тим швидше, чим більше їх швидкість. Процес ОУ 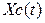ергодічний і стаціонарний, оскільки може бути одержаний в результаті лінійного інерційного перетворення білого шуму :

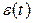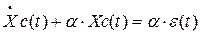
При моделюванні може бути використане наступне ітеративне співвідношення:

,

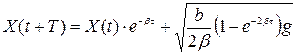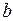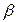де і – параметри процесу, а 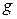– гаусова випадкова величина. Для нас найцікавіше, що даний процес, як затверджувалося раніше, має експоненціально спадаючу автокореляційну функцію: ,

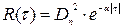де 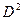– дисперсія, а спектр потужності має лоренцевській вигляд:

.

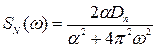У зв'язку з тим, що енергія зосереджена у області низьких частот, процес ОУ також називають кольоровий, рожевий шум. Спектральна густина має близьку до плоского ділянку в районі нуля частот і хвіст, що спадає по статечному закону в районі низьких частот.

Знайдемо сумарний сигнал:

.

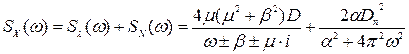Розглянемо спектральну густину шуму: .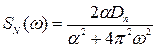

, ,

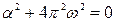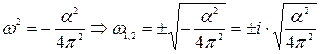Нехай 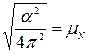, тоді знаменник дробу можна представити у вигляді .

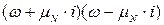Загальний сигнал:

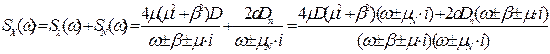
Виконаємо операцію факторизації:

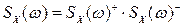
Для цього розглянемо спершу знаменник дробу:

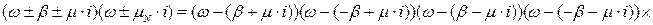
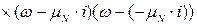
Представимо коріння на комплексній площині:

Після операції факторизації в знаменнику одержимо:

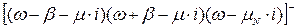
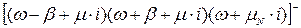
Виконаємо операцію сепарації для чисельника:

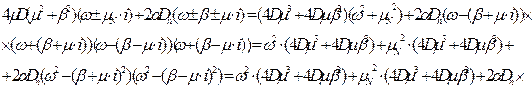
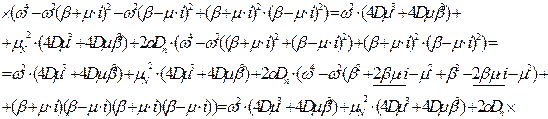
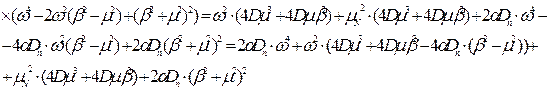
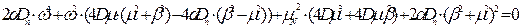
Виконаємо заміну до = 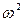, тоді:

.

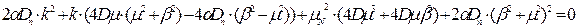
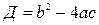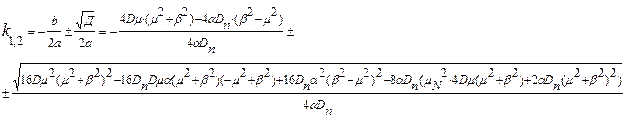
Зведемо в квадрат ліву і праву частину рівняння, щоб позбавитися квадратного коріння, заздалегідь проведемо заміни:

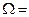
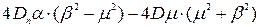
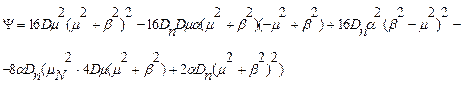
Тоді:

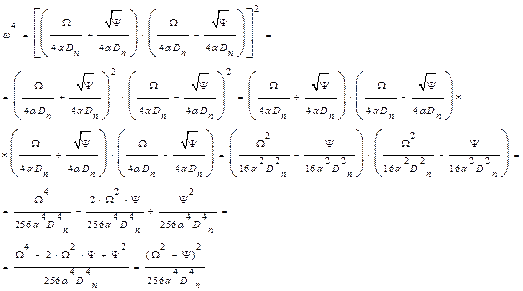
Звідси: .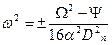

Повернемося до значень 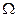і ψ:

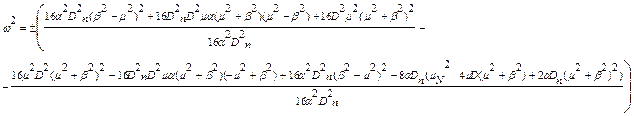
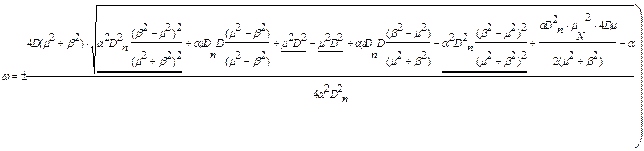
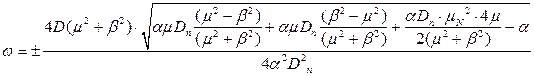
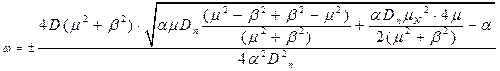
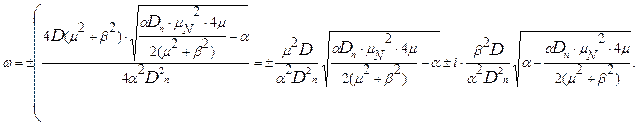
Нехай 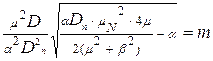, а ,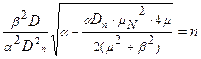

Тоді коріння чисельника: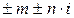

Запишемо факторізованную спектральну густину сумарного сигналу:

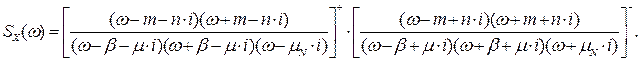Запишемо передавальну функцію сигналу в загальному вигляді:

.

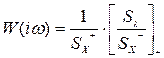Виробимо операцію сепарації з віражением:

.

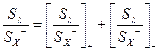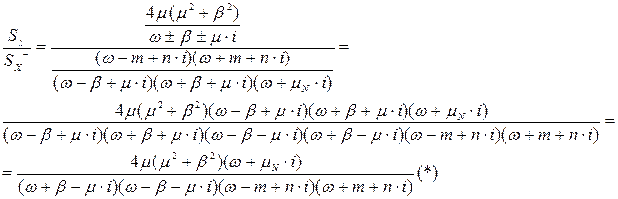
Вирішимо (*) методом невизначених коефіцієнтів:

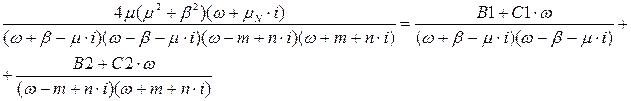
Помножимо обидві частини виразу на: .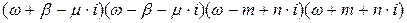

Одержимо:

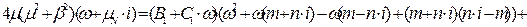
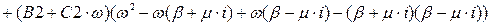
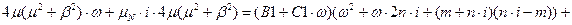
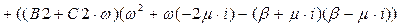
Складемо систему лінійних рівнянь:

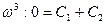
	(5.21)
w2: 0 = B1+ 2mi + C1(m + ni)(ni - m) + B2(-2mi) – C2(b + mi)(b - mi)	(5.22)
w1:4m(m2 + b2) = B1·2·mi + C1·(m + ni)(ni - m) + B2(-2mi) – C2(b + mi)(b - mi)	(5.23)
w0: mNi·4m(m2 + b2) = B1·(m + ni)(ni - m) – B2(b + mi)(b - mi)	(5.24)

Знайдемо рішення цієї системи:

А) З (5.21)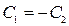

Б) З (5.22)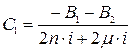

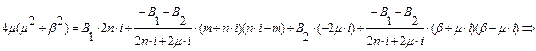
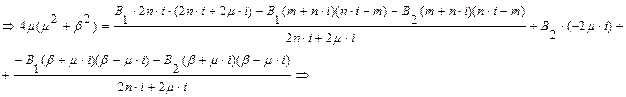
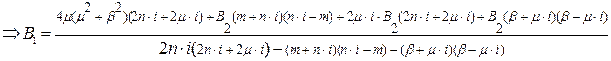
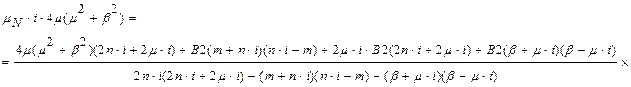
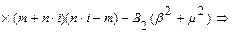
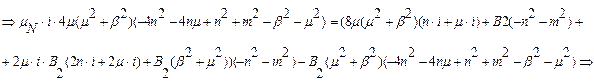
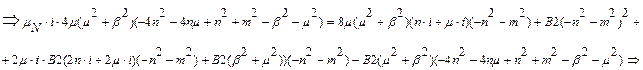
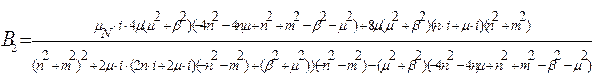
Знайдемо B₁ підставивши B₂:

=

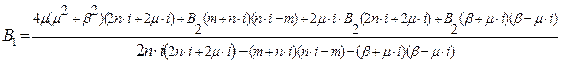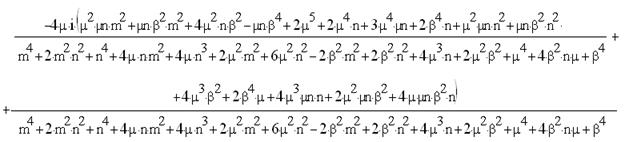
де .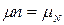

Підставивши В₁ і В₂ у вираз для С₁ одержимо:

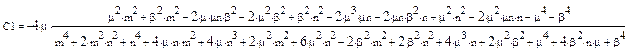
Аналогічно і С₂:

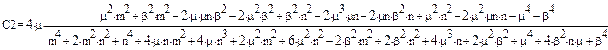
Передавальна функція прийме вигляд:

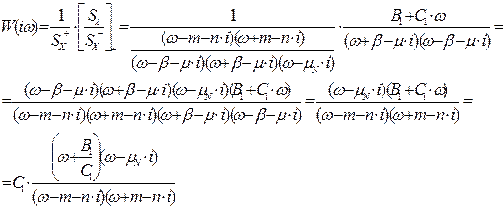
де

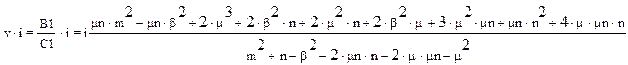Перейдемо до параметра p :

,

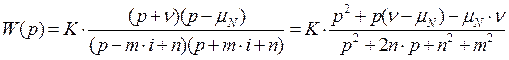де K=C₁

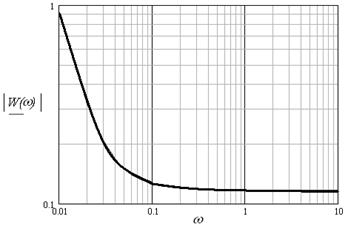
Рис. 5.2. Передавальна функція системи в логарифмічній системі координат.

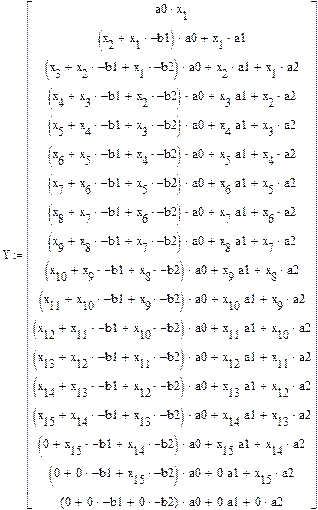
де x – час дискретизації. Матриця-стовпець, одержана при реалізації фільтру представленого на рисунку 5.2, є амплітудними значеннями сигналу в кожен момент часу.