Структура системи фільтрації червоної завади.
Сигнал є випадковим процесом, що диференціюється, з періодичною складовою. Його спектральна густина має вигляд:
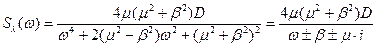
| де | m – | параметр загасання сигналу; |
| b – | резонансна частота корисного сигналу; | |
| a – | відносний рівень перешкоди. |
Для того, що б оцінити процес відбувається при дії перешкоди на корисний сигнал необхідно проаналізувати перешкоду що є кольоровим шумом. Спектральна густина перешкоди розглядається в цьому випадку, виявляє процесом Орнштейна-Улінбека (1930) є реалізацією випадкових кореляционних блукань. Процес Орнштейна-Улінбека ергодічеській і стаціонарний, оскільки може бути одержаний в результаті лінійного інерційного перетворення білого шуму .
Даний процес має експоненціально спадаючу автокореляционную функцію
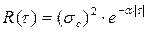
де 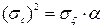 – дисперсія, де в свою чергу,
– дисперсія, де в свою чергу, 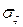 – дисперсія білого шуму.
– дисперсія білого шуму.
Спектральна густина перешкоди (спектр потужності) має наступний вигляд:
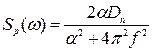 .
.
У зв'язку з тим, що енергія, зосереджена у області низьких частот процес Орнштейна-Улінбека, називають кольоровий (бурий або червоний) шум. Спектральна густина має близьку до плоского ділянку в районі нуля частот і хвіст, що спадає по статичному закону в районі високої частоти. Цим пояснюється двоякость даного процесу: при розгляді коротких реалізацій він представляється як класичний броунівський рух, а при спостереженні на великих тимчасових інтервалах має спектральні характеристики шуму.
Оскільки в даній задачі розглядається сигнал четвертого порядку те і шум матиме четвертий порядок.
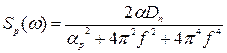 .
.
У даному виразі частота приведена в Гц, при переході вимірюванню радіану частоти спектральна густина перешкоди прийме вигляд:
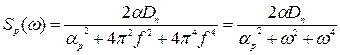
Порівняльна характеристика спектральної густини перешкоди (бурого шуму) другого і четвертого порядку приведені нижче (( 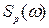 – 4-й порядок,
– 4-й порядок, 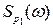 – 2-й порядок).
– 2-й порядок).
Рис. 5.3. Спектральна густина сигналу бурого (червоного) шуму
З графіка виходить, що спектральна густина перешкоди четвертого порядку має більш виражене зосередження енергії перешкоди в смузі нижніх частот.
Проаналізуємо спектральну густину перешкоди, тобто знайдемо полюси, прирівнявши знаменник до нуля:
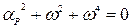
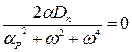
Позбавимося від 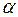 у чисельнику спектральної густини перешкоди, для чого поділимо і чисельник і знаменник на
у чисельнику спектральної густини перешкоди, для чого поділимо і чисельник і знаменник на 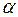 :
:
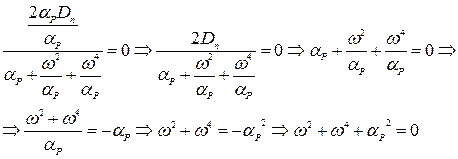 .
.
Коріння матиме наступний вигляд:
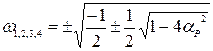 .
.
Знайдемо сумарну спектральну густину перешкоди і сигналу
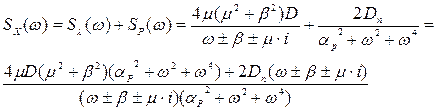 .
.
Для того, що б виконати операцію сепарації і факторизації, знайдемо коні чисельника (нулі) і знаменника (полюси), на підставі чого здійснимо розділення сумарної спектральної густини на спектральну густину реалізовуваної і нереалізовуваної систем.
Для виконання сепарації розглянемо знаменник дробу:
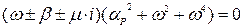 .
.
Для першого співмножника коріння матиме вигляд:
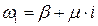
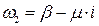
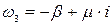
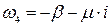 .
.
Для другого співмножника коріння виглядатиме таким чином (з розрахунків, приведених вище):
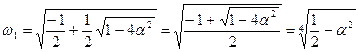
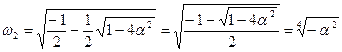
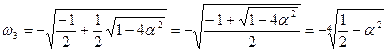

Для зручності запису, обчислень і аналізу одержаних функцій, зробимо заміну:
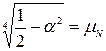 ;
; 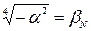 .
.
Тоді коріння матиме вигляд:
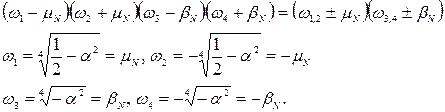
Знаходимо коріння чисельника (нулі):
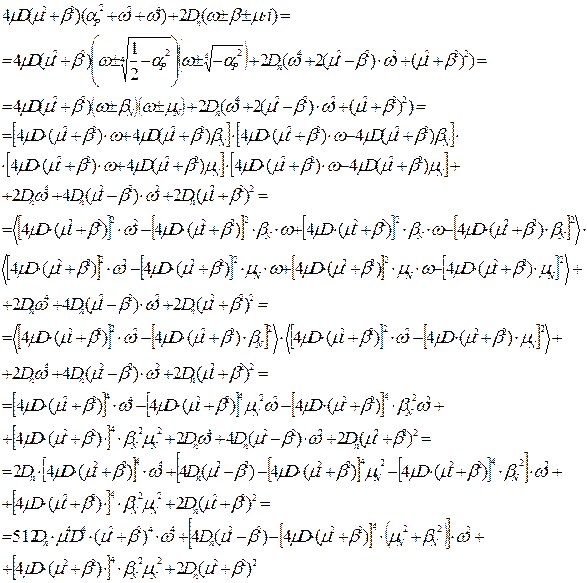
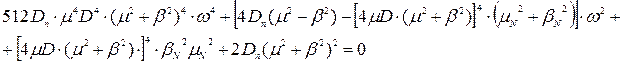
Чисельник має вигляд:
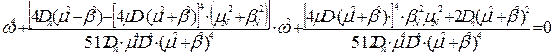 .
.
Зробимо заміну, ввівши позначення для наступних частин виразу, приведеного вище:
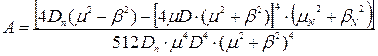 .
.
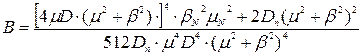 .
.
Вирішимо систему рівнянь:
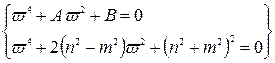 .
.
З якої знаходимо нові значення 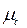 і
і 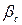 , за допомогою яких представимо коріння чисельника:
, за допомогою яких представимо коріння чисельника:
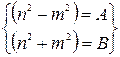 Звідки:
Звідки: 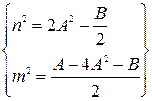 .
.
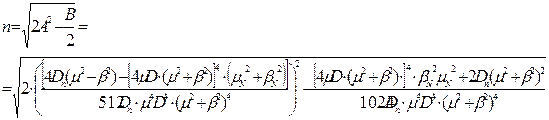
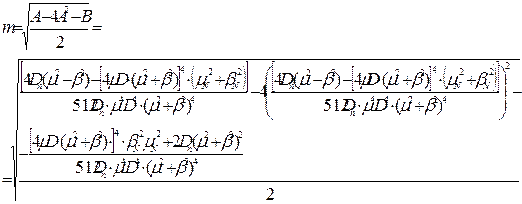
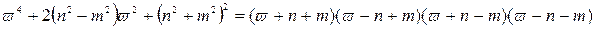
Коріння чисельника сумарного сигналу матиме наступний вигляд:
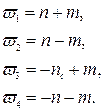
Запишемо факторизовану спектральну густину сумарного сигналу:
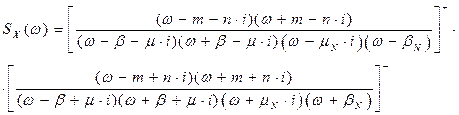
Функції фізично реалізовуваної 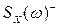 і не реалізовувана
і не реалізовувана 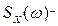 частини сумарної спектральної густини після операції сепарації матимуть вигляд:
частини сумарної спектральної густини після операції сепарації матимуть вигляд:
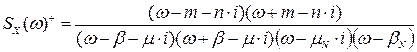
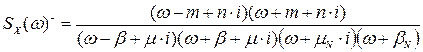 .
.
Функція, зворотна функції фізично реалізованої системи має вигляд:
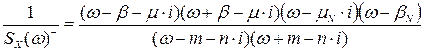
Передавальна функція фізично реалізованої системи має вигляд:
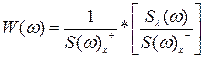 .
.
Для того, що б знайти передавальну функцію фізично реалізовуваної системи, необхідно зробити сепарацію і факторизацію другого співмножника у вигляді:
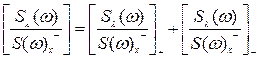
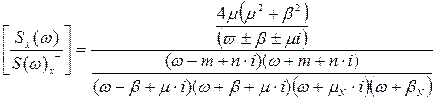 .
.
Після простих перетворень алгебри даний вираз прийме вигляд:
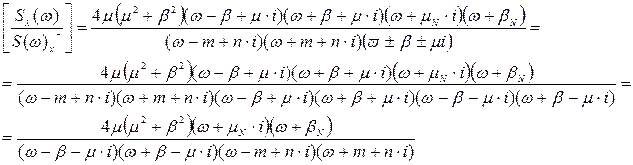
За допомогою методу невизначених коефіцієнтів виконаємо операцію сепарації приведеного вище виразу.
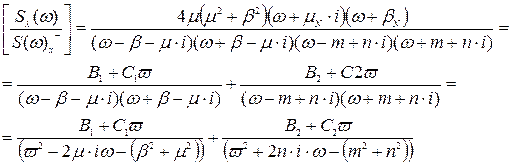
Перетворюваний чисельник:
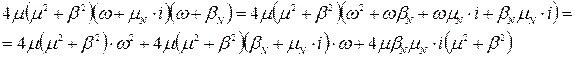
Визначаємо коефіцієнти B1, C1, B2, C2.
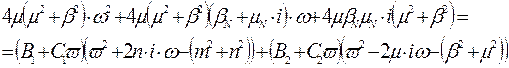
Складаємо систему рівнянні, прирівнюючи коефіцієнти при однакових ступенях:
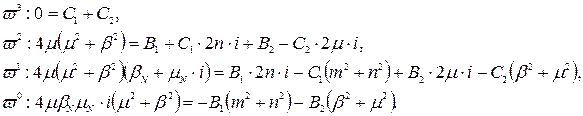

Вирішивши дану систему, знаходимо коефіцієнти:
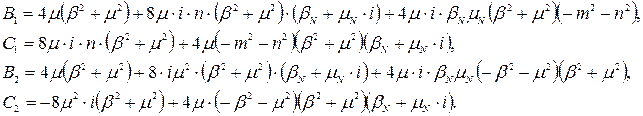
Після підстановки одержаних коефіцієнтів вираз матиме вигляд:
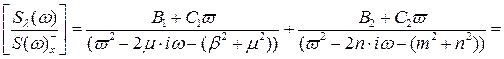
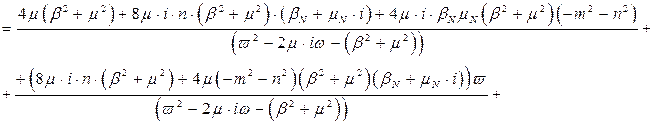
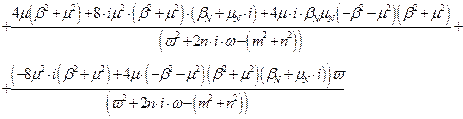
Оскільки полюси другого доданку одержаного виразу є фізично не реалізовуваною частиною, то після операції факторизації воно прийме вигляд:
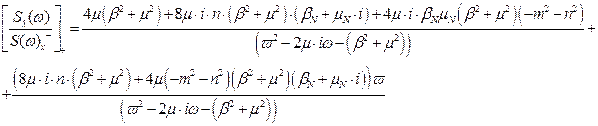
Не реалізована частина, в свою чергу матиме вигляд:
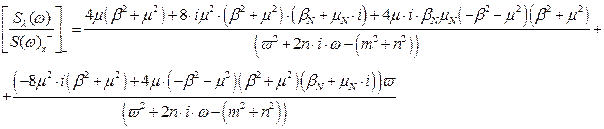
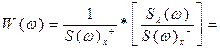
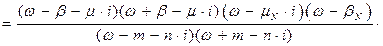
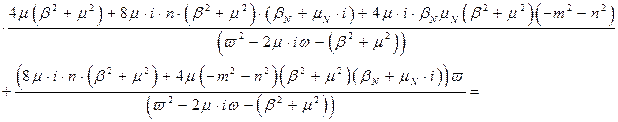
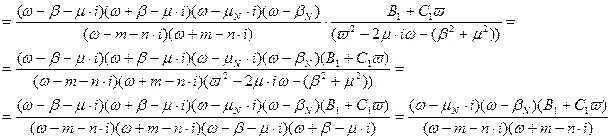
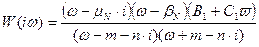
Переходимо до параметра 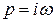 :
:
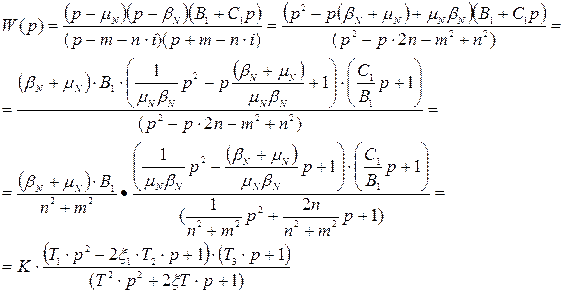
Коефіцієнт передавальної функції:
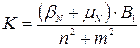 .
.
Постійні часу:
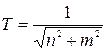 ,
, 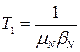 ,
, 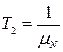 ,
, 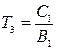
Відносний коефіцієнт затухання:
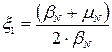 ,
, 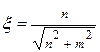
Аналізовані співвідношення:
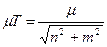 ,
, 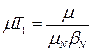 ,
, 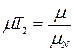 ,
, 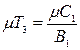
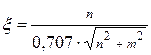
Проаналізуємо співвідношення постійної часу Т:
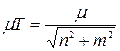
Яке після підстановки 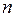 і
і 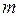 прийме вигляд:
прийме вигляд:
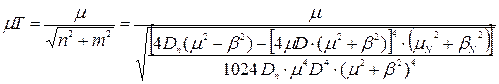
Оскільки 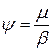 , то:
, то:
1) коли 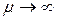 і
і 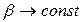 ,
, 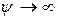 постійна часу
постійна часу 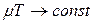 ;
;
2) коли 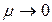 і
і 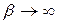 ,
, 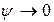 постійна часу
постійна часу 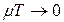 .
.
Таким чином, між ступенем регулярності 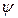 і співвідношенням
і співвідношенням 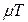 існує прямо пропорційна залежність.
існує прямо пропорційна залежність.
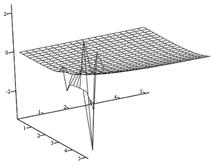
| Рис. 5.4. Залежність mT від дисперсій сигналу D і шуму Dn: 1) при D→ ∞ і Dn→ 0, постійна часу mT практично постійна ; 2) при D→ 0 і Dn→ ∞, постійна часу mT спостерігається та ж ситуація. 3) при D→ ∞ і Dn→ ∞, а постійна часу mT є фіксованим значенням різним для кожного випадку. |
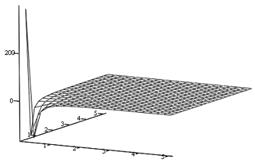
| Рис. 5.5. Залежність mT від параметрів mN і bN |
Проаналізуємо співвідношення постійної часу Т1:
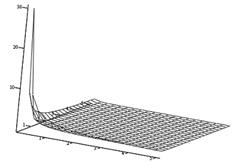
| Рис. 5.6. Залежність добутка mT1 від параметрів mN і bN: 1) при mN → ∞ і bN → 0, mT1 прагне до сталого значення; 2) при mN → 0 і bN → ∞, mT1 прагне до сталого значення; 3) при mN → 0 і bN → 0, mT1 зростає експоненціально до максимального значення. |
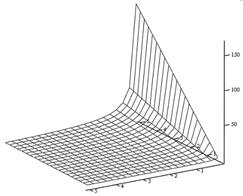
| Рис. 5.7. Залежність добутку mT1 від параметрів m і bN |
Проаналізуємо співвідношення постійної часу Т2:
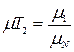 при обліку, що
при обліку, що 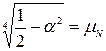 :
:
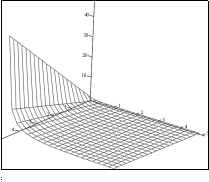
| Рис. 5.8. Залежність добутка mT2 від параметрів m і mN. |
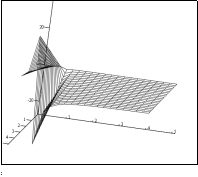
| Рис. 5.9. Залежність добутка mT2 від параметрів m і a. |
Проаналізуємо співвідношення постійної часу Т3:
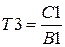
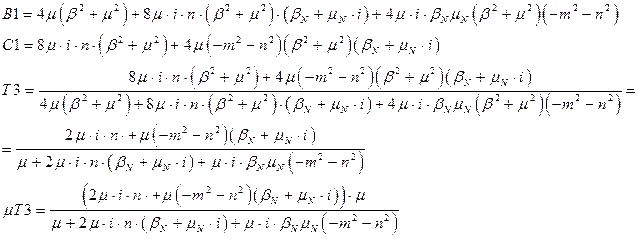
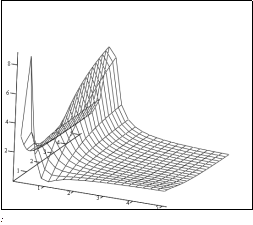
| Рис. 5.10. Залежність добутка mT3 від параметрів mN і bN |
Нижче приведені залежності добутка mT3 від параметрів m і b при різних значеннях bN.
При bN = 5
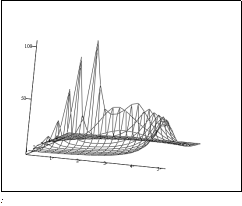
| Рис. 5.11. Залежність добутка mT3 від параметрів m і b. |
При bN = 1
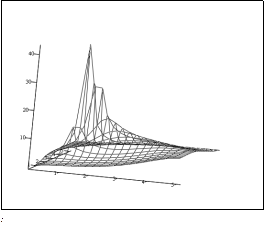
| Рис. 5.12. Залежність добутка mT3 від параметрів m і b. |
При bN = 0.1
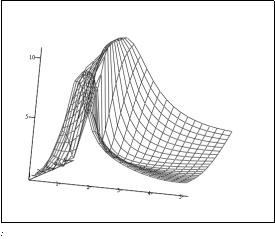
| Рис. 5.13. Залежність добутка mT3 від параметрів m і b |
При mN = bN = 0.1
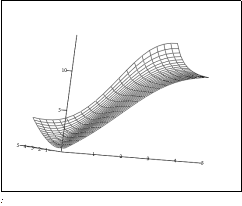
| Рис. 5.14. Залежність добутка mT3 від параметрів m і b. |
Проаналізуємо параметр x:
Заздалегідь здійснимо перетворення виразу для наочності і зручності побудови.
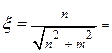
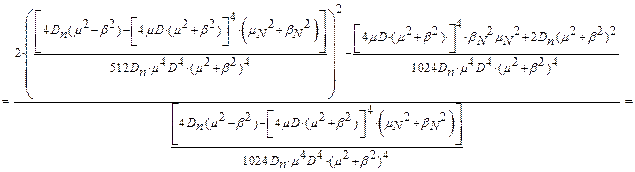
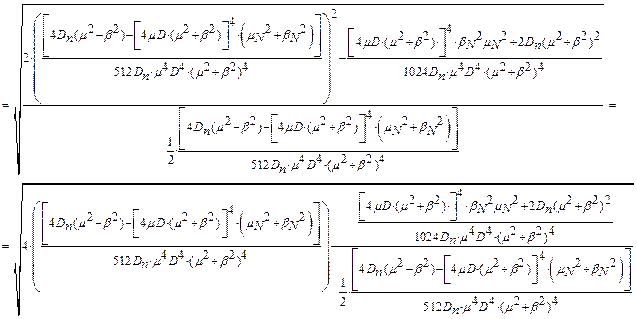
При заданих D і Dn
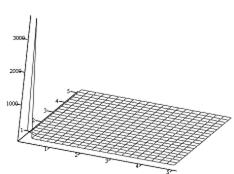
| Рис. 5.15. Залежність параметра x від параметрів m і b. |
Проаналізуємо параметрx1:
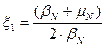
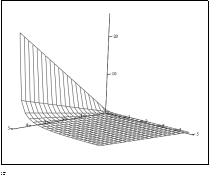
| Рис. 20. Залежність параметра x1 від параметрів mN і bN |
При обліку того, що 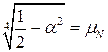 і
і 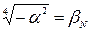 тоді
тоді 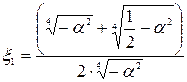 .
.
Контрольні запитання
1. Які перешкоди можуть виникати в системах керування?
2. Які існують види кольорових шумів?
3. Проаналізуйте вплив математичної моделі корисного сигналу та перешкоди на процес фільтрації.
4. Чим відрізняються моделі корисного сигналу і завади для випадку сигналів без періодичної складової? Наведіть їх формули.
5. Наведіть математичну модель білого шуму у випадку сигналів без періодичної складової.
6. Як впливає процес нормування на корисний сигнал та заваду?
7. Що таке частотна характеристика оптимального фільтра, як вона знаходиться?
8. Проаналізуйте зміну властивостей статистичного фільтра з ростом співвідношення перешкода/корисний сигнал. Зробіть висновки.
9. Висвітіть фізичну реалізіцію рожевої завади, наведіть її характеристику.
10. Для чого необхідно виконувати операції факторизації і сепарації?
11. Дайте характеристику методу невизначених коефіцієнтів.
12. Що таке цифрова реалізація фільтра?
13. Дайте визначення червоній заваді, наведіть її параметри.
14. Які відмінності між червоним шумом другого та четвертого порядка? Проілюструйте свою відповідь?
15. Проаналізуйте залежність добутку постійної часу на параметр затухання від безрозмірних параметрів.
16. Як визначається безрозмірні параметри передатної функції при синтезі фільтра червоних завад?
Дата добавления: 2015-06-27; просмотров: 681;
