Стохастична фільтрація в каналах вимірювання
Системи керування та наукових досліджень, де циркулює вимірювальна інформація, можуть містити некорельовані перешкоди, в тому числі і довільної форми. В колах керування джерелом перешкод є ЦАП та арифметично – логічні пристрої (АЛУ). В колах вимірювання - перешкода це кольоровий шум. Чим складніша процедура отримання початкової інформації тим більше завада відрізняється від білого шуму. Її математична модель може бути складніша за модель корисного сигналу. Тому задачу фільтрації вирішують для найбільш поширеного вузького набору вихідних характеристик. В найпростішому випадку сигналів без періодичної складової моделі корисного сигналу і завади співпадають за формою, але істотно відрізняюься за параметрами.
Для корисного сигналу:
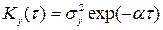
Для некорельованої перешкоди:
А) довільної форми 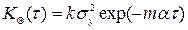
Б) білого шуму 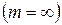
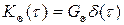 де
де 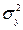 – дисперсія корисного сигналу;
– дисперсія корисного сигналу; 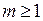 перешкода більш високочастотна, ніж корисний сигнал.
перешкода більш високочастотна, ніж корисний сигнал. 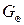 – інтенсивність білого шуму.
– інтенсивність білого шуму.
Приклад 1. Синтезуємо фільтр, котрий забезпечує виділення сигналу 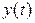 , спостерігаємого з перешкодою
, спостерігаємого з перешкодою 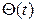 .
.
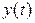 та
та 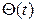 – некорельовані, тоді вхідний сигнал:
– некорельовані, тоді вхідний сигнал: 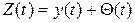 має характеристики:
має характеристики: 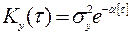 ;
; 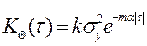 ,
,
Фур’є – вирази яких є 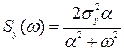 ;
; 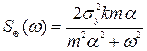 .
.
Нормування зменшує в 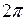 раз корисний сигнал, тоді його спектральна щільність:
раз корисний сигнал, тоді його спектральна щільність:
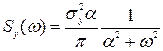 ,
,
а завади:
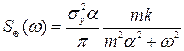 .
.
Ідеальний сигнал на виході в задачі відтворення сигналу на фоні завади:
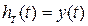 .
.
Область спостереження вхідного нескінченна, що практично відповідає умові значного перевищення інтервалу спостереження над часом корекції вхідного сигналу.
Частотна характеристика оптимального фільтра:
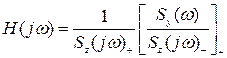 (5.1)
(5.1)
Спектральна щільність вхідного сигналу:
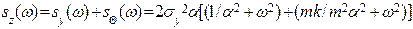 . (5.2)
. (5.2)
Після перетворень:
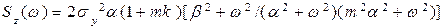 , (5.3)
, (5.3)
де:
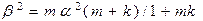 (5.4)
(5.4)
Проведемо факторизацію: 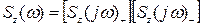 .
.
Звідки з врахуванням (5.3):
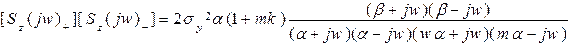
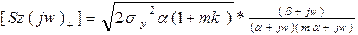 (5.5)
(5.5)
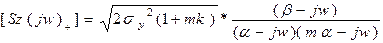
Далі, відповідно (5.1) та (5.5) та спектральної щільності:
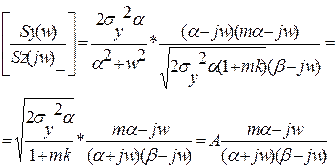 (5.6)
(5.6)
де: 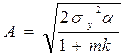 .
.
Сепарація останнього виразу:
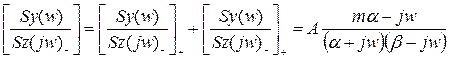 .
.
Розклавши (5.6) на дроби, отримаємо:
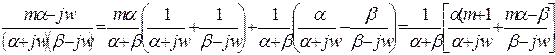 .
.
Тоді сепарований вираз відношення спектральних щільностей сигналу до факторизованої спектральної щільності зашумленого сигналу має вигляд:
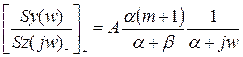 . (5.7)
. (5.7)
З (5.1), (5.5), (5.7) отримаємо оптимальну частотну характеристику статистичного фільтра:
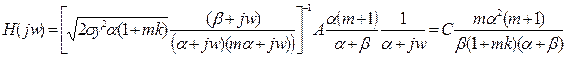 ,
,
де:
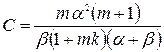 ;
; 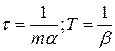 (5.8)
(5.8)
Звідки шукана функція статистичного фільтра:
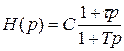 (5.9)
(5.9)
Таким чином, оптимальний статистичний фільтр - це інерційно - форсуюча ланка. Її суттєвий параметр – коефіцієнт відношення постійних часу форсування та інерційності:
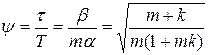 . (5.10)
. (5.10)
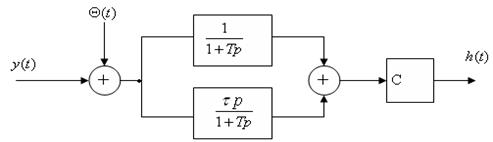
Рис. 5.1. Безперервний варіант оптимального статистичного фільтра за каналами виміру
Цей фільтр може бути уявлений у вигляді інерційного та інерційно – диференцюючих ланок з наступним проходженням сигналу через підсилювач з коефіцієнтом передачі, обумовленим величиною співвідношення дисперсій перешкода/корисний сигнал та зсувом цього співвідношення за фазою:
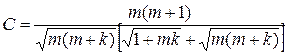 . (5.11)
. (5.11)
Прослідкуємо за деформацією властивостей статистичного фільтра по мірі росту співвідношення перешкода/корисний сигнал.
1) 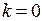 відсутність перешкоди. В цьому випадку з (5.9) – (5.11) слідує, що
відсутність перешкоди. В цьому випадку з (5.9) – (5.11) слідує, що 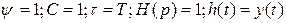 . Статистичний фільтр є безінерційний підсилювач з коефіцієнтом підсилення
. Статистичний фільтр є безінерційний підсилювач з коефіцієнтом підсилення 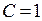 .
.
2) 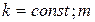 >>1 але так, що
>>1 але так, що 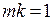 високочастотна перешкода. Тоді
високочастотна перешкода. Тоді 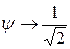 ;
; 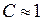 залишимо трохи менше 1.
залишимо трохи менше 1.
При рості 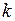 та падінні
та падінні 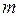 , але так, щоб
, але так, щоб 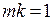 , коефіцієнт підсилення
, коефіцієнт підсилення 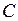 та ψзменшуються. Триває подальше зростання інерційно – інтегральних властивостей фільтра.
та ψзменшуються. Триває подальше зростання інерційно – інтегральних властивостей фільтра.
3) 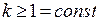 та
та 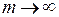 – істотно високочастотна перешкода. В цьому випадку
– істотно високочастотна перешкода. В цьому випадку 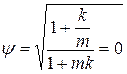 ;
; 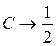 кінцево. Тоді
кінцево. Тоді 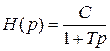 фільтр є чисто інерційною ланкою (інерційним підсилювачем).
фільтр є чисто інерційною ланкою (інерційним підсилювачем).
4) 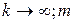 >1=const – нескінченно велика перешкода, тут
>1=const – нескінченно велика перешкода, тут 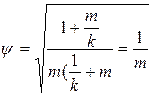 <<1;
<<1; 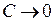 .Фільтр закриває вимірювальний канал від нескінченно великих перешкод.
.Фільтр закриває вимірювальний канал від нескінченно великих перешкод.
Ріст співвідношення перешкода/корисний сигнал веде до зростання інерційно – інтегральних властивостей фільтра. В границях 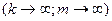 ці властивості спочатку інерційні, а потім фільтр спрацьовує як своєрідний вентиль з перемінною пропускною здатністю 0<
ці властивості спочатку інерційні, а потім фільтр спрацьовує як своєрідний вентиль з перемінною пропускною здатністю 0< 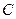 ≤1, відсікаючи вимірювальний канал від небажаних перетворень. Точність виділення корисного сигналу системою оцінюється середнім квадратом похибки
≤1, відсікаючи вимірювальний канал від небажаних перетворень. Точність виділення корисного сигналу системою оцінюється середнім квадратом похибки 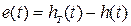 або
або 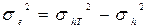 .
.
Тому що 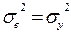 , то
, то 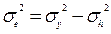 , (5.12)
, (5.12)
де
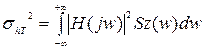 . (5.13)
. (5.13)
Виходячи з (5.11), квадрат модуля частотної характеристики оптимальної системи буде: 
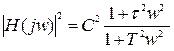 . (5.14)
. (5.14)
З врахуванням (5.2), отримаємо:
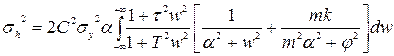 . (5.15)
. (5.15)
Після розкладення на елементарні дроби та перетворень, останній інтеграл прийме вигляд:
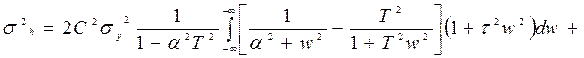
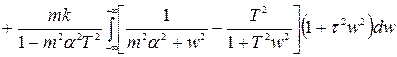 . (5.16)
. (5.16)
Після обчислення інтегралів:
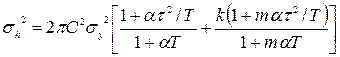 . (5.17)
. (5.17)
Підставляючи останній вираз в (5.12), визначимо середньоквадратичну похибку через параметри вхідного сигналу:
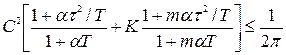 , (5.18)
, (5.18)
де параметри 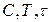 виражені формулами (5.4), (5.11), (5.18) одночасно визначає допустиму область змін параметрів перешкоди
виражені формулами (5.4), (5.11), (5.18) одночасно визначає допустиму область змін параметрів перешкоди 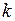 та
та 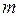 .
.
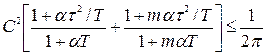 . (5.19)
. (5.19)
Тоді при 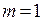 ,
, 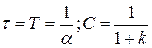 .
.
З формули (5.19) слідує, що:
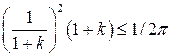 ,
,
або 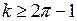 тобто припустима область визначення параметрів перешкоди є напівпряма:
тобто припустима область визначення параметрів перешкоди є напівпряма:
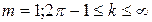 (5.20)
(5.20)
Підставивши параметри перешкоди 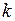 та
та 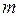 , котрі задовольняють припустимій області (5.20), в (5.18) знаходимо, що дисперсія помилки фільтрації
, котрі задовольняють припустимій області (5.20), в (5.18) знаходимо, що дисперсія помилки фільтрації 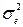 зростає від 0, при
зростає від 0, при 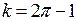 , до дисперсії корисного сигналу
, до дисперсії корисного сигналу 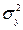 , при
, при 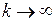 відповідно, тобто
відповідно, тобто 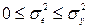 при
при 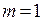 та
та 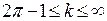 .
.
Дата добавления: 2015-06-27; просмотров: 627;
