Приклади стохастичного синтезу систем третього порядку.
Добуток випадкових процесів з періодичної (диференційний) і неперіодичною складовими дає корисний сигнал у вигляді:
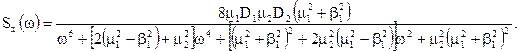
Сума корисного сигналу з перешкодою:
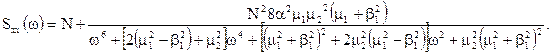
де 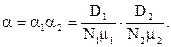
Розкладемо окремо чисельник і знаменник на добутки із шести членів кожний, або з трьох пар комплексно-спряжених коренів, із яких одна пара не має дійсної частини:
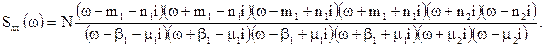
В другому вигляді:
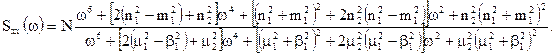
Рівняння мають однакові знаменники, а всі члени чисельника мають таку ж структуру, крім вільного члену. Тотожність чисельників можлива при умовах, коли постійні коефіцієнти і вільний член однакові, тобто:
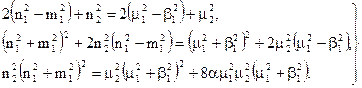 (4.32)
(4.32)
Праві частини трьох рівнянь відомі, як постійні параметри сигналу і перешкоди, а в лівій знаходяться три змінні, які треба знайти, так як вони показують розташування коренів чисельника.
Позначимо відомі значення коефіцієнтів:
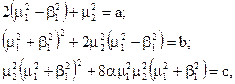
а невідомі через:
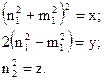
Тоді система рівнянь має вигляд:
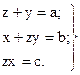 (4.33)
(4.33)
Знайдемо невідомі. З останнього рівняння z=c/x, тоді:
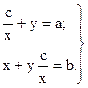 .
.
Оскільки y=a-c/x, тоді з останнього рівняння одержали:
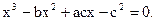 (4.34)
(4.34)
Використаємо відоме рішення Кардано, коли підстановка x=r-b/3 приводить до вигляду: 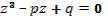 .
.
Тут
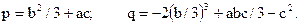
Корені неповного рівняння:
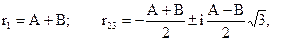
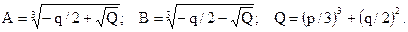
Знайшовши дійсний корінь 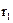 , визначили х, потім із третього рівняння системи – z, а з першого – у.
, визначили х, потім із третього рівняння системи – z, а з першого – у.
По умові 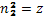 , а
, а 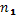 і
і 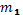 знайдемо із рівнянь:
знайдемо із рівнянь:
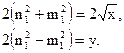
Знайдемо суму, тоді:
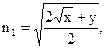
а відповідна різниця дає:
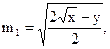
Таким чином визначено координати всіх нулів спектральної щільності сумарного сигналу.
Розглянемо більш загальний вигляд мультипликативного корисного сигналу, який включає добуток двох випадкових процесів з періодичною складовою, апроксимованих диференційними функціями, та адитивної перешкоди:
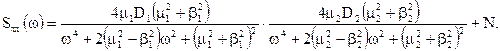
В іншому вигляді:
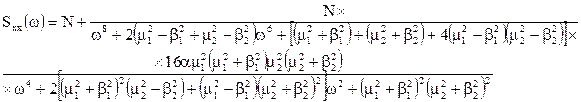 .
.
Тут 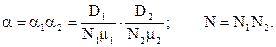
Розкладаємо окремо чисельник і знаменник на добутки із восьми простих членів, кожний із яких включає чотири комплексно-спряжені, причому одна пара комплексно-спряжених коренів має всього два параметри – дійсну та уявну частини:
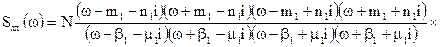
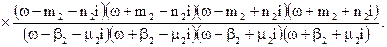
В вигляді двох добутків поліномів четвертого ступеня:
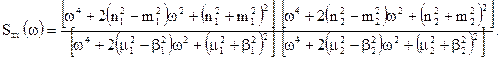
Розкривши дужки, одержали:
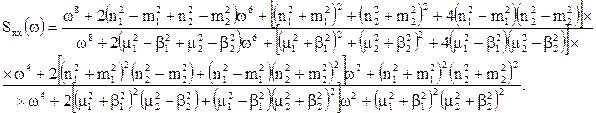
Тотожність рівнянь можлива, коли постійні коефіцієнти та вільні члени однакові, тобто:
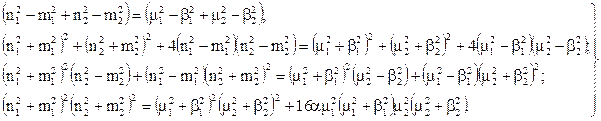
Чотири рівняння включають чотири невідомі параметри n1, m1, n2, m2 праві частини відомі по визначенню сигналів.
Позначимо відомі параметри сигналів:
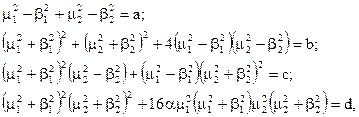
Тут 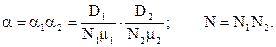
а вирази із невідомих параметрів позначимо так:
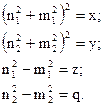
Тоді система чотирьох рівнянь має вигляд:
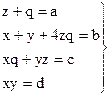 .
.
Знайшовши невідомі параметри останньої системи рівнянь, визначимо невідомі параметри коренів чисельника, оскільки корені знаменника нам відомі по визначенню.
Коливальні процеси, що проходять в об'єктах та системах керування, описуються диференційними рівняннями, які мають порядок вище другого. Найпростішою моделлю є ланка другого порядку. Перетворення, наприклад, ланкою другого порядку бiлого шуму приводить на виходi до спектральної щiльностi, вiдповiдної диференцiйовному випадковому процесу.
Операцiя сепарацiї може бути виконана на основi теореми Кошi про лишки. В цьому випадку знаходиться часова функцiя U(t) як зворотне перетворення Фур'є функцiї U(p) = 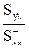 :
: 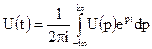 .
.
Iнтеграл знаходимо як суму лишкiв за всiма полюсами пiдiнтегральної функцiї, яка має полюси як в правiй, так i в лiвiй напiвплощинi. Якщо PK - полюси кратностi 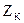 , розташованi в лiвiй напiвплощинi, i
, розташованi в лiвiй напiвплощинi, i 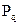 – полюси порядку
– полюси порядку 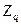 , розташованi в правiй напiвплощинi, то:
, розташованi в правiй напiвплощинi, то:
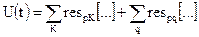 , (4.35)
, (4.35)
де
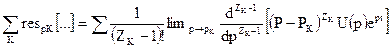 ,
,
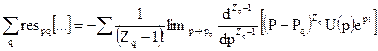 .
.
Знак мiнус у другої суми обумовлений вiд'ємним напрямком обходу контура, що охоплює праву напiвплощину.
Оскiльки перетворення Фур'є функцiї часу, яка дорiвнює нулю при t<0, являється аналiтичним в правiй напiвплощинi, знайдем перетворення Фур'є вiд функцiї 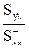 :
:
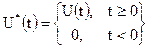 . (4.36)
. (4.36)
Перетворення Фур'є функцiї 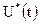 , що спiвпадає з перетворенням Лапласу, яке має всi смуги в лiвiй напiвплощинi, представляє собою шукану сепаровану функцiю
, що спiвпадає з перетворенням Лапласу, яке має всi смуги в лiвiй напiвплощинi, представляє собою шукану сепаровану функцiю 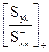 .
.
Дата добавления: 2015-06-27; просмотров: 685;
