Дослідження вільної складової руху системи
На значення дисперсiї помилки системи автоматичного регулювання, усередненої за нескiнченно великий промiжок часу, слабо впливають помилки, пов'язанi з вiдносно короткочасними перехiдними процесами. Тому параметри замкнутої системи повиннi вибиратися з врахуванням помилок в перехiдних режимах.
Як випадковi функцiї характеризуються дисперсією, так детермiнованi сигнали характеризуються інтегральною квадратичною оцінкою. Слід вказати на iзоморфнiсть задач стохастичної фiльтрацiї Колмогорова - Вiнера i задачi аналiтичного конструювання регуляторів, незважаючи на те, що цi задачi на перших порах вирiшувались зовнi рiзними способами. Інтеграл виду:
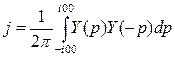 (6.10)
(6.10)
де j – iнтегральна оцiнка якостi;
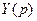 – перетворення Лапласа, формально має ту ж природу, що й iнтеграл (6.1).
– перетворення Лапласа, формально має ту ж природу, що й iнтеграл (6.1).
Наявнiсть протирiч мiж умовами пiдвищення точності систем автоматичного регулювання в усталеному i перехiдному режимах приводить до того, що зменшення вимушеної складової помилки по вiдхиленню викликає погiршення перехiдного процесу. Якщо параметри замкнутої системи вибранi iз умов мiнiмiзацiї середньоквадратичної помилки, то система може мати слабозатухаючий перехiдний процес.
Треба знайти область параметрiв випадкових вхiдних процесiв, коли мiнiмiзацiя динамiчних помилок виконується в межах статистичного синтезу автоматично. Перехiдна функцiя оптимальної динамiчної системи має вигляд:
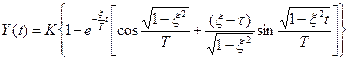 , (6.12)
, (6.12)
де Т – постiйна часу замкнутої системи;
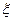 – вiдносний коефiцiєнт затухання замкнутої системи;
– вiдносний коефiцiєнт затухання замкнутої системи;
t= 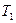 /T – вiдношення постiйних часу.
/T – вiдношення постiйних часу.
Відносне відхилення дорівнює:

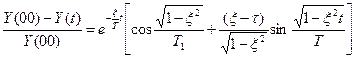 (6.13)
(6.13)
В іншій формі:
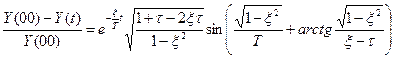 . (6.14)
. (6.14)
Амплiдуда вiдносного вiдхилення дорiвнює:
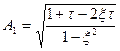 . (6.15)
. (6.15)
Для передаточної функцiї, в котрiй вiдсутнiй нуль, амплiтуда вiдносного вiдхилення визначається виразом:
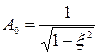 . (6.16)
. (6.16)
З урахуванням (6.6), амплiтуда вiдносного вiдхилення форсованої системи має вигляд:
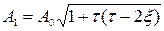 . (6.17)
. (6.17)
Значення амплiтуди вiдносного вiдхилення необмежено зростає, якщо 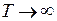 , тобто коли нуль прямує до початку координат.
, тобто коли нуль прямує до початку координат.
Положення нуля, при якому амплiтуда вiдносного вiдхилення буде наiменшою, визначається iз умови:
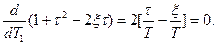
Звiдки: 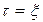 . (6.18)
. (6.18)
При виконаннi умови (6.18) мiнiмальне значення амплiтуди вiдносного вiдхилення дорiвнює одиницi.
Умова мiнiмiзацiї амплiтуди вiдносного вiдхилення в задачi статистичного синтезу оптимальних i квазiоптимальних систем для диференцiйовного випадкового процесу має вигляд:
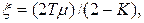 (6.19)
(6.19)
де 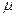 – параметр затухання автокореляцiйної функцiї процесу;
– параметр затухання автокореляцiйної функцiї процесу;
К – коефiцiєнт передачi замкнутої системи;
Пiдставляючi значення параметрiв, отримали умову (6.19) у виглядi:
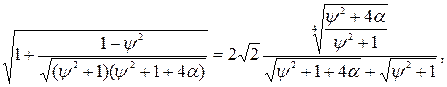 (6.20)
(6.20)
де 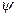 – ступень регулярності процесу;
– ступень регулярності процесу;
 – вiдношення дисперсiй процесу i перешкоди у смузi процесу.
– вiдношення дисперсiй процесу i перешкоди у смузi процесу.
При 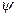 = 0,
= 0,  = 4,2, а при
= 4,2, а при  =0,
=0, 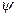 = 1.
= 1.
Для недиференцiйовного випадкового процесу мнiмiнiзацiя амплiтуди вiдносного вiдхилення у вiдповiдностi з (6.18) визначається умовою:
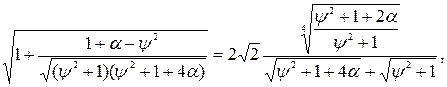 (6.21)
(6.21)
яка задовольняється при нульових ступеню регулярностi i вiдношеннi дисперсiй процесу i перешкоди. Для всiх iнших значень параметрiв випадкових процесiв умова (6.21) не виконується, тобто параметр вiдношення постiйних часу завжди бiльше, нiж вiдносний коефiцiєнт затухання, тому положення нуля неоптимальне i мiнiмiзацiя амплiтуди вiдносного вiдхилення не виконується.
Таким чином, у задачi точної прокатки профiлiв оптимiзацiя динамiчних систем покритерiю мiнiмуму середньоквадратичної помилки забеспечує умови, коли одночасно забеспечується мiнiмiнiзацiя амплiтуди вiдносного вiдхилення. Якщо для оптимальних i квазiоптимальних систем, одержаних на основi диференцiйовного випадкового процесу, ступiнь регулярностi випадкового процесу i вiдношення дисперсiй процесу i перешкоди в смузi процесу зв'язанi спiввiдношенням (6.20), то забеспечуються умови одночасної оптимiзацiї по двох критерiях: мiнiмума середньоквадратичної помилки i амплiтуди вiдносного вiдхилення. В оп-тимальних i квазiоптимальних динамiчних системах, отриманних на основi недиференцiйовного випадкового процесу, зазначена умова, у вiдповiдностi з спiввiдношенням (6.21), виконується при  = 0 i
= 0 i 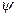 = 0.
= 0.
Для форсованої системи другого порядку знайшли максимальне вiдхилення iз умови:
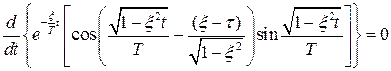 .
.
Момент часу при якому має місце максимум дорівнює:
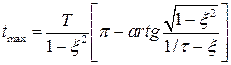 (6.22)
(6.22)
Тодi перерегулювання має вигляд:
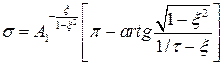 (6.23)
(6.23)
Представляють інтерес залежнiсть перерегулювання вiд ступеня регулярностi диференцiйовного випадкового процесу при постiйному значеннi дисперсiй процесу i перешкоди в задачах оптимального i квазiоптимального синтезу. Перерегулювання у нефорсованiй системi значно менше, нiж у форсованiй. Статистичний синтез на основi диференцiйовного випадкового процесу приводить до того, що в областi ступеня регулярностi рiвного одиницi перерегулювання в нефорсованiй системi не залежить вiд вiдношення дисперсiй, а у форсованiй слабо залежить вiд нього. При збiльшеннi ступеня регулярностi перерегулювання збiльшується тим бiльше, чим менше вiдношення дисперсiй процесу i перешкоди. При зменшеннi ступеня регулярностi ψ < 1 перерегулювання навпаки зменшується, але тим сильнiше, чим менше вiдношення дисперсiй процесу i перешкоди.
Для апроксимацiй, вiдповiдних недиференцiйовному випадковому процесу, перерегулювання збiльшується з ростом ступеня регулярностi процесу i зменшенням вiдношення дисперсiй процесу i перешкоди, причому перерегулювання в системi без форсування менше, нiж в оптимальнiй форсованiй системi.
Перерегулювання у форсованiй системi, отриманiй для диференцiйовного випадкового процесу, бiльше, нiж для недиференцiйовного, що посилюється з ростом вiдношення дисперсiй процесу i перешкоди. Якщо вiдношення дисперсiй нульове, перерегулювання в обох випадках однаковi.
Якщо нуль вибрано так, щоб забеспечувалась мiнiмальна амплiтуда вiдносного вiдхилення, що вiдповiдає умовам (6.10) i (6.11), то перерегулювання має вигляд:
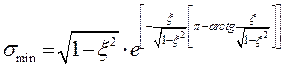 . (6.24)
. (6.24)
Вiдносний коефiцiєнт затухання i коливальнiсть пов'язанi
спiввiдношенням:
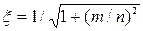 , (6.25)
, (6.25)
де n, m – параметри комплексних коренiв суми корисного сигналу i перешкоди;
m/n – коливальнiсть системи.
Тодi перерегулювання у системi з оптимально розташованим нулем має вигляд:
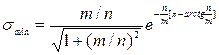 .
.
Коливальнiсть системи автоматичного регулювання, отриманої на основi диференцiйовного випадкового процесу, з врахуванням (2.33), дорiвннює:
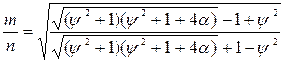 . (6.26)
. (6.26)
При ступенi регулярностi диференцiйовного процесу рiвному одинiцi iснує вузлова точка, де коливнiсть системи дорiвнює одиницi i не залежить вiд вiдношення дисперсiй процесу i перешкоди. Зi збiльшенням ступеня регулярностi процесу коливальнiсть збiльшується тим бiльше, чим менше вiдношення дисперсiї процесу до дисперсiї перешкоди, взятої в смузi процесу. Зi зменшенням ступеня регулярностi процесу коливальнiсть зменшується тим сильнiше, чим менше вiдношення дисперсiй процесу i перешкоди. Якщо вiдношення дисперсiй процесу i перешкоди дорiвнює нулю,то коливальнiсть системи дорiвнює ступеню регулярностi процесу. Якщо вiдношення дисперсiї процесу до дисперсiї перешкоди, взятої в смузi процесу, дорiвнює нескiнченностi, то коливальнiсть системи дорiвнює одиницi.
Коливальнiсть систем, одержаних для апроксимацiї, вiдповiдної недиференцiйовному випадковому процесу, на основi рiвнянь (6.25), має вигляд:
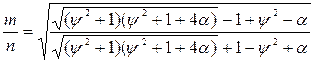 . (6.27)
. (6.27)
Коливальнiсть тим бiльше, чим вище ступiнь регулярностi процесу i менше вiдношення дисперсiй процесу i перешкод у смузi процесу. Коливальнiсть систем являється важливою динамiчною характеристикою, проте не враховує розмiщення нуля. Тому являється повною характеристикою нефорсованих систем.
Для оцiнки динамiчних властивостей форсованих систем визначили показник коливальностi, як вiдносне значення максимума амплiтудно-частотної характеристики замкнутої системи:
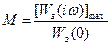 ,
,
де 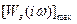 – максимальне значення модуля амплiтудно-частотної характеристики замкнутої системи;
– максимальне значення модуля амплiтудно-частотної характеристики замкнутої системи;
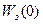 – значення модуля при w = 0.
– значення модуля при w = 0.
Модуль амплiтудно-частотної характеристики записали у виглядi:
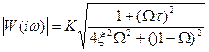
де 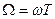 – вiдносна частота;
– вiдносна частота;
w – частота.
Максимум модуля визначили iз умови:
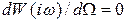 .
.
Вiн досягається при значеннi вiдносної частоти:
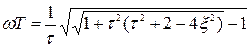 . (6.28)
. (6.28)
Форсована ланка другого порядку перетворюється в коливальну в тому випадку, коли вiдносна частота приймає доданковi значення, тобто 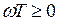 , що досягається при умовi:
, що досягається при умовi:
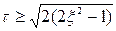 . (6.29)
. (6.29)
При 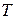 = 0, коли ланка трансформується в коливальну, вiдносний коефiцiєнт затухання знаходиться в межах 0 < x > 0,707. При наявностi форсуючої постiйної часу область iснування коливальних ланок розширюється тим бiльше, чим бiльше вiдношення постiйних i часу ланки. Наприклад, при t =1,41 i x = 1 ланка знаходиться на межi коливальностi, при t>1,41 перетворюється в коливальну, а при t <1,41 стає аперіодичним.
= 0, коли ланка трансформується в коливальну, вiдносний коефiцiєнт затухання знаходиться в межах 0 < x > 0,707. При наявностi форсуючої постiйної часу область iснування коливальних ланок розширюється тим бiльше, чим бiльше вiдношення постiйних i часу ланки. Наприклад, при t =1,41 i x = 1 ланка знаходиться на межi коливальностi, при t>1,41 перетворюється в коливальну, а при t <1,41 стає аперіодичним.
Показник коливальностi має вигляд:
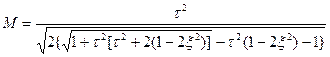 . (6.30)
. (6.30)
Мiнiмальне значення показника коливальностi дорiвнює одиницi при ступенi регулярностi диференцiйовного процесу, що змiнюється в дiапазонi вiд нуля до одиницi i збiльшується зi збiльшенням ступеня регулярностi при зменшеннi вiдношення дисперсiй процесу i перешкоди.
Аналогiчна картина спостерiгається для недиференцiйовного процесу. Графiки в задачах оптимального i квазiоптимального синтезу спiвпадають.
Показник коливальностi нефорсованих систем автоматичного
регулювання:
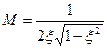 ,
, 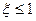 . (6.31)
. (6.31)
Показник коливальностi вiд ступеня регулярностi для диференцiйовних i недиференцiйовних процесiв вiдповiдно при постiйному значеннi вiдношеня дисперсiй процесу i перешкоди. Мiнiмум дорiвнює одиницi i спостерiгається для диференцiйовного процесу при ступенi регулярностi, що змiнюється в диапазонi вiд нуля до одиницi. Показник коливальностi тим бiльше, чим менше вiдношення дисперсiй процесу i перешкоди. Для недиференцiйовного процесу вказаний дiапазон розширюється i змiщується в область бiльших значень ступеня регулярностi з збiльшенням вiдношення дисперсiй процесу i перешкоди.
Застосування лiнiйних iнтегральних оцiнок якостi перехiдних процесiв доцiльне тiльки для монотонних перехiдних процесiв. Враховуючi, що синтезованi системи автоматичного регулювання по критерiю мiнiмума середньоквадратичної помилки характеризуються малими значеннями перерегулювання при великому затуханнi, застосування вказаних оцiнок представляється обгрунтованим. Однак, припустимий дiапазон змiн ступеня регулярностi тим бiльше, чим вище вiдношення дисперсiй процесу до перешкоди. У задачi оптимального i квазiоптимального синтезу для диференцiйовного процесу перерегулювання збiльшується, тим бiльше, чим менше вiдношення дисперсiй.
Iнтегральнi оцiнки обчислюються шляхом iнтегрування сигналу перехiдного процесу. Лiнiйна iнтегральна оцiнка дорiвнює:
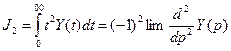 ,
,
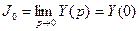 .
.
Для систем автоматичного регулювання, маючих iнтегральну складову, що вiдповiдає передавальнiй функцiї розiмкнутої системи у виглядi (2.68), отримали:
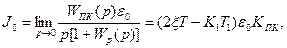 (6.32)
(6.32)
де J0 – лінійна інтегральна оцінка якості;
Wp(p) – передавальна функцiя розiмкнутої системи;
WПК(р) – передавальна функцiя прямого кола;
e0 – помилка системи.
Таким чином, лiнiйна iнтегральна оцiнка пропорцiйна 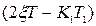 Зі збільшенням ступеня регулярностi випадкового процесу оцiнка зменшується тим бiльше, чим нижче вiдносний рiвень перешкод. Для диференцiйовного випадкового процесу абсолютне значення лiнiйної iнтегральної помилки найменше, спiвпадає для оптимального i квазiоптимального синтезу i дорiвнює
Зі збільшенням ступеня регулярностi випадкового процесу оцiнка зменшується тим бiльше, чим нижче вiдносний рiвень перешкод. Для диференцiйовного випадкового процесу абсолютне значення лiнiйної iнтегральної помилки найменше, спiвпадає для оптимального i квазiоптимального синтезу i дорiвнює 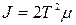 .
.
Лiнiйна iнтегральна оцiнка якостi перехiдного процесу для недиференцiйовного випадкового процесу бiльше, нiж для систем, одержаних для диференцiйовного процесу Лiнiйна iнтегральна оцiнка дорiвнює:
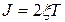 ,
,
i при вiдношеннi дисперсiй процесу i перешкоди рiвному нулю має вигляд:
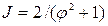 .
.
Зi збiльшенням вiдношення дисперсiй процесу i перешкоди лiнiйна iнтегральна оцiнка зменшується у випадку диференцiйовного процесу в бiльшому ступеню для малих значень ступеня регулярностi (наприклад, рiвних нулю) i збiльшується при великих значеннях вказаного параметра.
Розглянемо вплив параметрiв випадкового процесу на час регулювання. Для задоволення вимоги до швидкостi затухання процесу необхiдно виконати умову:
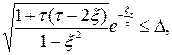
де D – задане значення вiдносного зменшення ординати перехiдного процесу.
Оцiнка часу регулювання має вигляд:
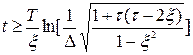 . (6.33)
. (6.33)
Для оптимального нуля, у вiдповiдностi за умовою (6.18), отримали:
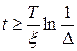 . (6.34)
. (6.34)
Для диференцiйовного випадкового процесу оптимальна динамiчна система забеспечує час регулювання:
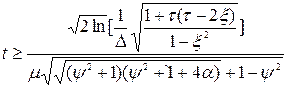 . (6.35)
. (6.35)
При вiдношеннi дисперсiї процесу до дисперсiї перешкоди рiвному безкiнечностi час регулювання дорiвнює нулю, поскiльки постiйна часу дорiвнює нулю. Якщо вказане вiдношення дорiвнює нулю, то час регулювання не залежить вiд ступеня регулярностi процесу i визначається як 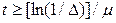 . Зокрема при
. Зокрема при 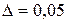
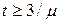 .
.
Коли ступiнь регулярностi процесу дорiвнює нулю, час регулювання визначається виразом:
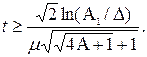
Для умов квазiоптимального i оптимального синтезу перешкодозахищеннiсть автоматичних систем на основi диференцiйовного випадкового процесу побудованi залежностi добутку часу регулювання на параметр затухання вiд ступеня регулярностi процесу при постiйному вiдношеннi дисперсiй процесу i перешкоди. Слабко виражений мiнiмум вказаного добутку змiщується в область зростаючих значень ступеня регулярностi при збiльшеннi вiдношення дисперсiй процесу i перешкоди, зменшуючись за величиною.
Чим бiльше ступiнь регулярностi диференцiйовного процесу i вiдношення дисперсiй процесу i перешкоди, тим менше вказаний добуток.
Для аналiтичної функцiї випадкового процесу, вiдповiднiй недиференцiйовному процесу, час регулювання визначається виразом:
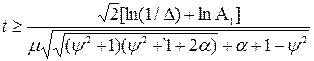 . (6.36)
. (6.36)
В задачах оптимального i квазiоптимального синтезу залежностi повнiстю спiвпадають. Указаний добуток в функцiї ступеня регулярностi процесу має мiнiмум, котрий змiщується в область бiльших значень ступеня регулярностi при збiльшеннi вiдношення дисперiй процесу i перешкод. Чим бiльше вiдношення вказаних дисперсiй, тим менше добуток часу регулювання на параметр затухання.
Крива перехідного процесу являється асимптотичним настроюванням шуканого коефіцієнта передачі, її можна отримати аналітичним шляхом. Оцінка часу перехідного процесу дозволяє оцінити кількість необхідних ітерацій, коли значення коефіцієнту відрізняється від фактичного на величину заданої помилки.
З врахуванням формул для визначення часу, при якому має місце максимум перехідної функції, і для визначення параметра затухання знаходимо відношення часів досягнення максимуму перехідної функції і першого мінімуму автокореляційної функції у вигляді:
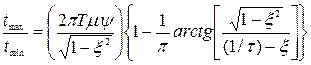 . (6.37)
. (6.37)
Наприклад, для одиничного ступеня регулярності диференційованого випадкового процесу і відношенні дисперсій процесу до перешкоди рівнім нулю знаходимо, що в форсованій системі Тμ=0,7; ξ=0,707; τ=0,7, а шукане відношення дорівнює 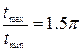 .
.
Таким чином, час досягнення максимуму перехідної функції настроювання шуканого коефіцієнта передачі пропорційний часу досягнення мінімуму автокореляційної функції процесу.
На основі формули для визначення моменту часу, при якому перехідна функція визначення коефіцієнта передачі має помилку регулювання, що не перевищує А, з врахуванням формули для визначення параметра затухання випадкової функції процесу, знайшли відношення часів регулювання в форсованій системі з заданою помилкою і досягнення першого мінімуму автокореляційної функції у вигляді:
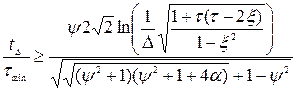 (6.38)
(6.38)
де D − помилка регулювання;
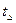 − час досягнення заданого значення, коли помилка не перевищує допустимого значення;
− час досягнення заданого значення, коли помилка не перевищує допустимого значення;
t − відношення постійних часу перешкодостійкої системи;
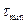 − час досягнення першого мінімуму автокореляційної функції.
− час досягнення першого мінімуму автокореляційної функції.
Відносний час визначення асимптотичного настроювання коефіцієнта передачі тим менше, чим більше відношення дисперсій процесу і перешкоди і менше амплітуда відносного відхилення А1, що визначається формулою (6.5).
Аналогічне відношення для нефорсованої системи:
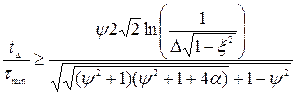 . (6.39)
. (6.39)
Для умов попереднього прикладу при 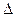 = 0,05:
= 0,05:
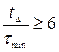 ,
, 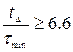
Якщо відношення дисперсій процесу і перешкоди дорівнює нулю, а амплітуда відносного відхилення дорівнює одиниці, що відповідає умовам приклада, то для форсованої системи можна записати:
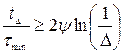 . (6.40)
. (6.40)
Відношення часу асимптотичного настроювання до часу мінімуму автокореляційної функції пропорційне ступеню затухання випадкового процесу, зокрема, при D=0,05:
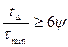 .
.
Для умов прикладу, коли α = 5, отримаємо Тμ= 0,4; τ = 0,9.
Тоді при ∆= 0,05:
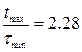 ;
; 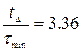 ;
; 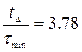 .
.
Кількість ітерацій n, необхідних для отримання коефіцієнта з заданою помилкою D, визначається добутком отриманого відношення і відношення q часів досягнення мінімуму автокореляційної функції процесу і зсуву реалізації випадкового процесу, кратного одному вимірюванню:  .
.
Тоді: 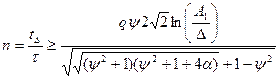 (6.41)
(6.41)
Наприклад, якщо 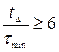 , а q =10, то кількість ітерацій n > 10.
, а q =10, то кількість ітерацій n > 10.
Дата добавления: 2015-06-27; просмотров: 669;
