Послідовне ввімкнення елементарних ланок

При послідовному з'єднанні ланок вихідна величина попередньої ланки поступає на вхід подальшого.

Метод факторизації (LU-перетворення)

Розв`язування лінійних рівнянь виконується або прямими, або ітераційними методами. Нижче будуть розглядатися тільки прямі методи розв`язування. До прямих методів відносяться метод Гауса та метод факторизації. Розглянемо метод факторизації (LU-перетворення).

Нехай є система лінійних рівнянь:

,

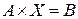яку можна записати в матричному вигляді:

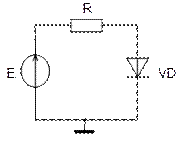
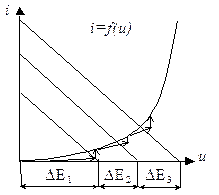
Рис. 7.2. – Метод рухомої області збіжності: а – схема з діодом;

б – графічна ілюстрація її розрахунку методом рухомої області збіжності.

Формально цю систему рівнянь можна вирішити, обернувши матрицю А: X=A^-1×B.

.

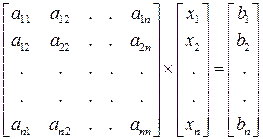Однак, така операція трудомістка і вимагає великих затрат машинного часу Т_маш. Чисельне розв`язання систем лінійних рівнянь часто базується на методі Гауса. Він ґрунтується на тому факті, що додавання одного рівняння системи до іншого, помноженого на константу, не змінює рішення.

Виключення за Гаусом вимагає виконання n3/3 операцій, де під операцією розуміється комбінація множення та віднімання, а n – порядок матриці. Зворотна підстановка вимагає n2/2 операцій.

Однак, кращим методом розв`язування систем лінійних алгебраїчних рівнянь є метод перетворення (розкладу) матриці А на трикутні матриці, або метод LU- перетворення (факторизації). Алгоритм цього методу близький до методу Гауса.

Головна перевага методу LU-перетворення в порівнянні з методом Гауса – це можливість більш простого отримання рішень для різноманітних векторів в правій частині системи рівнянь.

Припустимо, що матрицю СЛАР можна розкласти на множники A=L·U, де

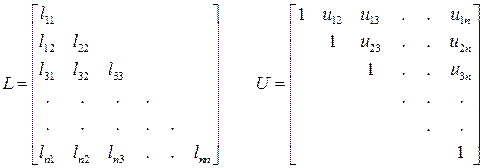
Тут матриця L є нижньою трикутною, а матриця U – верхньою трикутною. Помітимо, що на головній діагоналі матриці U знаходяться одиниці. Це означає, що визначник матриці А дорівнює добутку діагональних елементів l_ii матриці L.

Припустимо, що ми отримали матриці L та U. Тоді: L×U×X=B

Позначимо U×X=Z, тоді ми отримаємо: L×Z=B.

Завдяки спеціальній формі матриці L, вектор Z можна легко визначити. Для цього запишемо:

l₁₁z₁ = b₁,

l₂₁z₂+l₂₂z₂ = b₂,

l₃₁z₃+l₃₂z₃+l₃₃z₃ = b₃,

l_n1z₁+l_n2z₂+l_n3z₃+...+l_nn z_n= b_n.

Звідси одержуємо:

z₁ = b₁/l₁₁,

z₂ = (b₂ - l₂₁z₁)/l₂₂,

z₃ = (b₃ – l₃₁z₁ – l₃₂z₂)/l₃₃, …

Або в загальному вигляді:

z₁=b₁/l₁₁;

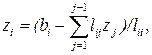i = 2, 3,..., n.

Цей процес називається прямим виключенням (прямою підстановкою або прямим ходом). Щоб ці обчислення мали сенс, діагональні елементи lii повинні бути ненульовими. Тепер повернемось до U·X=Z і знайдемо вектор X.

x₁+u₁₂x₂+u₁₃x₃+...+u_1nx_n = z₁,

x₂+u₂₃x₃+...+u_2nx_n = z₂,

………………….......

x_n-1+u_n-1,n x_n = z_n-1,

x_n = z_n.

Починаючи з останнього рівняння, послідовно знаходимо компоненти вектора X. В загальному вигляді вони визначаються за формулою:

x_n=z_n,

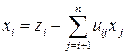, i = n–1, n–2,..., 1.

Цей процес називається зворотною підстановкою, або зворотним ходом. Число операцій, необхідних для виконання як прямої підстановки, так і зворотної, дорівнює n2/2, а в сумі для розв`язування СЛАР вимагається n2 операцій. Виведенням формул LU-перетворення займатися не будемо. Наведемо загальні вирази для отримання елементів матриць L та U:

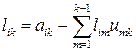, i = k, k+1,..., n,

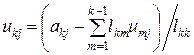, j = k+1, k+2,..., n.

Важливі переваги методу LU-перетворення:

1. Легко обчислюється визначник матриці А:

.

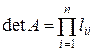2. Елементи матриці L та U можуть бути записані на місця елементів матриці А і занесені в ті ж самі осередки пам'яті (запам'ятовувати одиничні елементи на головній діагоналі матриці U немає необхідності).

3. Легко знайти рішення для іншого вектору B у правій частині, тобто не потрібно повторно проводити LU-перетворення, а достатньо провести пряму та зворотну підстановки.

4. Для рівнянь з транспонованою матрицею A^t X=C рішення знаходиться при тому ж LU-перетворенні. Аналіз таких систем рівнянь необхідний при розрахунку чутливості.

Число операцій, необхідних для LU-розкладу, складає (n³/3-n/3) і разом з прямою та зворотною підстановками еквівалентно методу Гауса. Однак він більш прийнятний із-за переваг, зазначених вище.