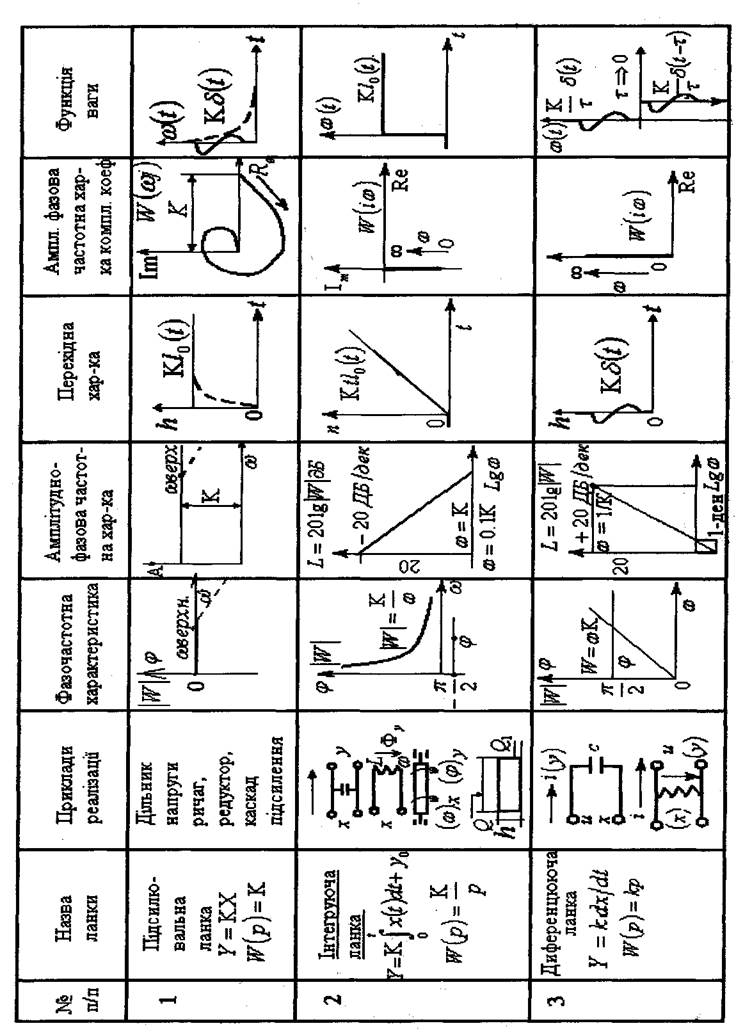
Основи класифікації ланок.
Перехідний процес любої ланки може бути записаний в загальному випадку диференційним рівнянням.
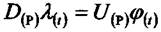
В подальшому будемо передбачати, що диференційне рівняння ланки дано в безрозмірній формі.
В залежності від порядку рівняння ланок можуть бути нульового, першого, другого й більш високих порядків.
До простих відносяться ланки до 2 порядку. Класифікація простих ланок відбувається
або по диференційному оператору 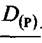 виходу ланки або по вигляду передатної функції
виходу ланки або по вигляду передатної функції
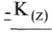 . Перша класифікаціярозглядає структуру ланки з точки зору його вільних
. Перша класифікаціярозглядає структуру ланки з точки зору його вільних
коливань без врахування збурюючих дій. Такий підхід може бути корисним при рішенні різних питань, що стосуються стійкості ланки. Друга класифікаціяпо передатній функції більш поглиблена, вона точніше враховує характерні особливості ланки. Якщо притримуватися другої нормалізованої форми диференціального рівняння, то
класифікація по вихідному оператору може бути обмежена 12 видами полінома 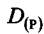 ;
;
тобто:
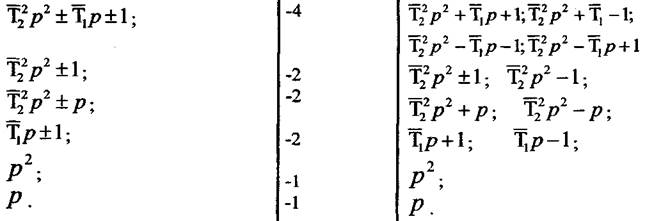
Ланки оператори які мають додатний вільний член, рівний одиниці, називають статичним. Якщо вільний член відсутній, ланка називається остаточною.
Ланки оператори яких мають від'ємний вільний член, рівний одиниці, класифікуються як володіючі від'ємним статизмом.
Ланка з вихідним оператором типу 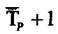 називається одноємнісною так як
називається одноємнісною так як
одноємнісні елементи мають завжди рівняння типу 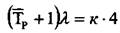 . Ланка з оператором
. Ланка з оператором
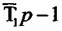 є нестійкою, тому що єдиний корінь характеристичного рівняння завжди додатній, що як було сказано раніше приводить до нестійкого руху ланки.
є нестійкою, тому що єдиний корінь характеристичного рівняння завжди додатній, що як було сказано раніше приводить до нестійкого руху ланки.
Ланка, що має оператора 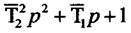 , носить назву коливальної при умові, що
, носить назву коливальної при умові, що
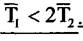 При
При 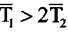 ланка може бути розложеною на дві послідовно з'єднаних
ланка може бути розложеною на дві послідовно з'єднаних
ланки типу 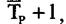 тобто на дві одноємостних ланки.
тобто на дві одноємостних ланки.
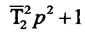
|
| , називають консервативною. Особливості цієї ланки |
Ланка з оператором 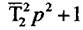 , називають консервативною. Особливості цієї ланки
, називають консервативною. Особливості цієї ланки
полягають в тому, що вона створює при збурюючих діях нестихаючі коливання, тому що
обидва кореня характеристичного рівняння 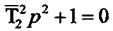 є чисто уявними числами.
є чисто уявними числами.
Ланки з оператором Р є інтегруючою, що витікає з рівняння
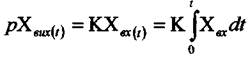 . Особливість цієї ланки є її властивість давати реакцію на
. Особливість цієї ланки є її властивість давати реакцію на
виході пропорційну значенню інтеграла від вхідної функції. Сигнал отриманий на виході ланки при подачі на його вхід одиничного імпульсу 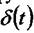 , називається ваговою, або
, називається ваговою, або
імпульсною, перехідною функцією 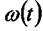 . В цьому випадку зображення по Лапласу
. В цьому випадку зображення по Лапласу
вхідного сигналу 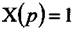 , а зображення вихідного сигналу співпадає з передатною
, а зображення вихідного сигналу співпадає з передатною
функцією. 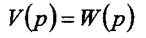
Переходимо від зображення до оригіналу і отримуємо вагову функцію.
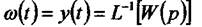
тобто вагова функція є оригіналом передатної функції. Так як зображення вагової функції 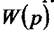 відрізняється зображення передатної функціїтільки
відрізняється зображення передатної функціїтільки 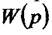 множником Р,
множником Р,
то 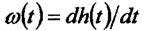
Таким чином, перехідну функцію завжди можна знайти вагову функцію;
- перехідна-
- вагова- 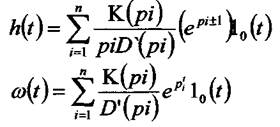
Ланка з оператором 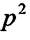 може бути розкладена на дві послідовно з'єднані інтегруючі ланки. Ланка, яка має оператор
може бути розкладена на дві послідовно з'єднані інтегруючі ланки. Ланка, яка має оператор 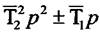 , може бути представлена як послідовна
, може бути представлена як послідовна
комбінація з двох ланок: 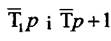 де
де  тобто як послідовне з'єднання
тобто як послідовне з'єднання
остаточної та одноємнісної ланок.
Перейдемо тепер до класифікації по передатній функції.
|
 від
від  , матимемо "сімейство" векторів. Криву, проведену через кінці радіусів -
, матимемо "сімейство" векторів. Криву, проведену через кінці радіусів -
векторів на комплексній площині, називають амплітудою — фазовою частотною характеристикою (АФЧХ).
АФЧХ характеризує зміну амплітуди коливань вихідної величини і зсуву фаз між вихідними та вхідними сигналами від частоти при незмінній амплітудівхідного гармонійного діяння.
Залежність зміни амплітуди вихідного сигналу від частоти показує 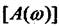 і
і
фазочастотною 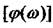 характеристиками. Підставимо у вихідне диференційне рівняння
характеристиками. Підставимо у вихідне диференційне рівняння
значення вихідної і вхідної величин і візьмемо похідну за часом:
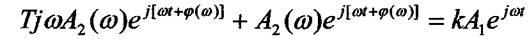
Поділимо добуте рівняння на 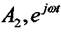 ,винесемо за дужки спільні члени і з урахуванням
,винесемо за дужки спільні члени і з урахуванням
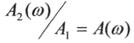 запишемо
запишемо
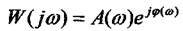
порівнюючи з попередніми виразами, або виглядами цієї величини
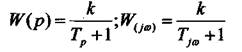
визначимо, що математичний вираз для комплексного коефіцієнта передачі можна добувати, коли підставити 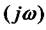 замість оператора Р у формулу передатної функції.
замість оператора Р у формулу передатної функції.
Підставимо у рівняння і 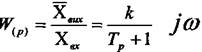 замість Р, позбавимося у виразі
замість Р, позбавимося у виразі
комплексності в знаменнику та відокремимо дійсну та уявну частини.

Обидва додатки залежать від частоти і є окремими характеристиками, які будують при зміні частоти від 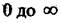 . Вираз який не має уявності називають дійсною частотою
. Вираз який не має уявності називають дійсною частотою
характеристики.
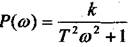 >а додаток у якому є
>а додаток у якому є 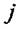 - уявною (мнимою) частотною характеристикою.
- уявною (мнимою) частотною характеристикою.
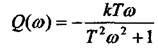
Підставляючи значення частоти від 0 до 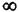 у вирази
у вирази 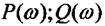 можна побудувати
можна побудувати
дійсну та уявну характеристики у функції частоти.
За парами значень Р і Q для окремих частот можна побудувати на комплексній площині амплітудно - фазову характеристику.
АФЧХ можна побудувати також за значеннями 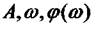
Дата добавления: 2015-05-16; просмотров: 1233;
