Амплітудна частотна характеристика.

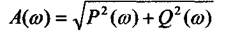
Фазова частотна характеристика:

Лекція №3. Вираз, який не має уявності, називають дійсною частотною характеристикою.

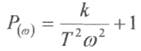
а додаток у якому є комплексна величина 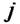^— уявною частотною характеристикою.

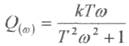
змінюючи ( ^_ частоту) від 0 до можна побудувати дійсну й уявну характеристики і функції частоти. За парами значень P,Q для окремих частот можна побудувати на комплексній площині амплітудно-фазову частотну характеристику.

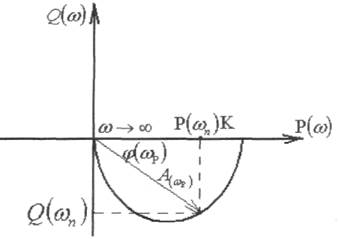
Амплітудна частотна характеристика, яка випливає з рисунку;

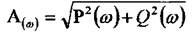
Фазова частотна характеристика;

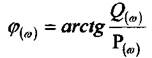
Використовуючи рівняння 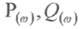дістанемо;

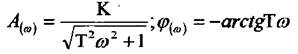
Прологарифмуємо вираз:

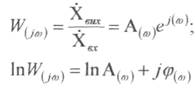, за виразом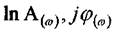

будуємо відповідно логарифмічну амплітуду (ЛАЧХ) і фазову (ЛФЧХ) частотні характеристики, які істотно спрощують дослідження систем автоматичного регулювання, їх будують із застосуванням зручніших на практиці десяткових логарифмів.

По шкалі частот замість 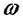відкладають 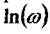. Логарифмічна шкала відносно

частоти 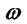нерівномірна, а відносно 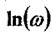- рівномірна.

Основними одиницями логарифмічної шкали є декада і октава.

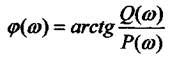
Використовуючи рівняння , дістанемо:

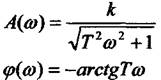
Якщо прологарифмувати 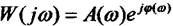отримаємо

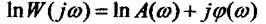
За виразами 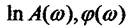будуть відповідно логарифмічною амплітудою, тобто ЛАЧХ

і логарифмічно — фазовою, а отже АФЧХ частотними характеристиками.

Октава-це інтервал частот між якимсь значенням частоти і її подвоєним значенням. Отже, октава зображується відрізком, що має однакову довжину на будь-якій ділянці

шкали. Довжина відрізка дорівнює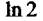

Декада-інтервал частот між певним значенням частоти та її значенням, збільшеним у 10 разів. Зображується декада відрізком завдовжки 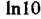, це відрізок одиничної довжини,

оскільки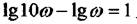

По осі ординат відкладають не 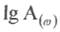, а пропорційну йому величину

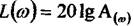, яку вимірюють у децибелах.

1 Децибел (дБ)- це 0.1Б (бел)- одиниці логарифмічної величини, що являє собою логарифм безрозмірного відношення фізичної величини до однойменної фізичної величини, яку вважають вихідною.

Змінна відношення двох величин у 10 разів відповідає зміні підсилення на 20дБ.

Враховуючи, що 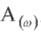є відношенням амплітуди коливань на вході виході, змінна

підсилення на 20дБ відповідає змінні відношення двох амплітуд у 10 разів. При відношенні двох величин, що дорівнюють 1, підсилення в децибелах дорівнює 0,

оскільки

Якщо відношення вихідного і вхідного коливань менше 1, підсилення в логарифмічному масштабі буде негативним, що означає ослаблення сигналу на виході порівняно зі входом.

При побудові логарифмічних фазових частотних характеристик по осі ординат відкладають значення кутів у натуральній величині, а по осі абсцис частоту 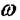по логарифмічній шкалі.

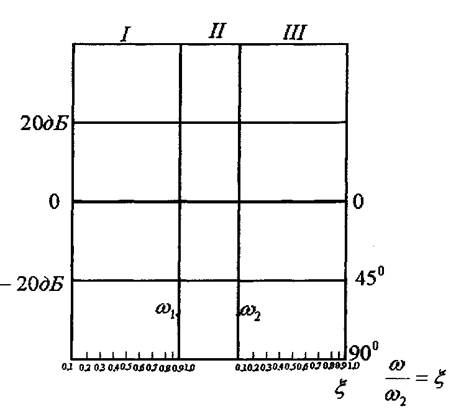
Прологарифмуємо вираз і дістанемо логарифмічну амплітудну частотну характеристику ЛАЧХ.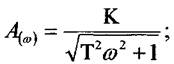

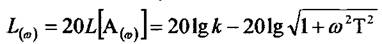
Логарифмічну характеристику будують починаючи з

ЛАЧХ.

частоти розміщуються по мірі їх

можливості

Передатна функція 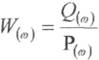може бути представлена у вигляді відношення у якої

чисельник і знаменник розкладені на множники з поліномів першого або другого ступеню в залежності з яких ланок складена досліджуємо модель системи. Звідси витікає, що побудова фазових і амплітудних характеристик може бути виконана шляхом побудови відповідних характеристик окремих ланок з наступним їх додаванням приймаючи до уваги їх знак (- або +).