Керування.
На практиці перехідні процеси різних за своїми фізичними принципами дії ланок (елементів) визначаються подібними диференціальними рівняннями динаміки, що дає можливість класифікувати їх за виглядом рівнянь динаміки. Наприклад, з цієї точки зору, до одного типу елементів можна віднести такі, на перший погляд, різні елементи, як механічна рухома маса і електричне активно -індуктивне коло.
Так, рівняння динаміки для механічної маси з моментом інерції 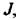 можна записати у вигляді:
можна записати у вигляді:
або при 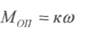
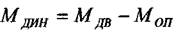
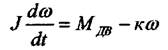
 |
Групуючи вихідні величини в лівій частині рівняння, а вхідні - в правій, дістаємо:
Рівняння динаміки активно - індуктивного кола з електричним активним опором R та індуктивністю L матиме вигляд:
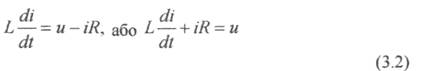
Рівняння (3.1) і (3.2) мають аналогічний вигляд, тому характер зміни струму і та швидкості 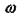 в перехідних режимах цих елементів буде аналогічним і за класифікацією, прийнятою в теорії автоматичного керування, ці елементи відносять до одного й того ж типу.
в перехідних режимах цих елементів буде аналогічним і за класифікацією, прийнятою в теорії автоматичного керування, ці елементи відносять до одного й того ж типу.
З лівої частини рівняння елемента, в якій представлені вихідна величина та її похідні, видно, як швидко та точно реагує елемент на вхідну величину, що записується в правій частині рівняння.
Наявність похідних у лівій частині рівняння показує, що елемент поступово реагує на вхідну величину, перехідний процес діє певний час, коли є відхилення вихідної величини від заданого рівня.
Якщо похідних у лівій частині рівняння динаміки елемента нема, то це означає, що елемент миттєво реагує на вхідну величину.
Похідні можуть бути не тільки в лівій частині рівняння динаміки елемента, а й у правій.
У загальному випадку права частина рівняння динаміки елемента показує, на що реагує даний елемент і з яким коефіцієнтом передачі (підсилення) вхідна величина з'являється на виході елемента.
Залежно від вигляду правої частини рівняння елемент (ланка) може реагувати: на саму вхідну величину; тільки на похідну від вхідної величини; на інтеграл від вхідної величини; на вхідну величину та її похідну; на вхідну величину та інтеграл від неї; на вхідну величину, похідну та інтеграл від неї. Можливі йінші варіанти вигляду правої частини рівняння.
Основними динамічними характеристиками елементів є:
- часова характеристика хвих = f(t);
- перехідна функція 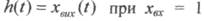 , що показує, яким чином
, що показує, яким чином
елемент реагує на одиничне значення вхідної величини;
- функція ваги, що є похідною від перехідної функції
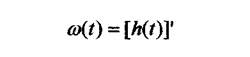
| Крім названих характеристик елементів, важливими характеристиками є передаточні функції W(p) та різні частотні характеристики елементів, докладніше про які буде сказано далі. Відповідно до рівнянь динаміки розрізняють типові динамічні ланки. |
Крім названих характеристик елементів, важливими характеристиками є передаточні функції W(p) та різні частотні характеристики елементів, докладніше про які буде сказано далі.
Відповідно до рівнянь динаміки розрізняють типові динамічні ланки.
Безінерцінна (підсилювальна) лавка.її називають також ідеальним елементом. Він має як в динаміці, так і статиці однакове рівняння
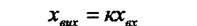
| Це рівняння показує, що вхідна величина миттєво, без будь - яких відхилень, надходить на вихід елемента з передаточним коефіцієнтом к. Прикладом таких елементів можуть бути механічні редуктори, які не мають люфтів, електронні лампи та ін. |
Це рівняння показує, що вхідна величина миттєво, без будь - яких відхилень, надходить на вихід елемента з передаточним коефіцієнтом к. Прикладом таких елементів можуть бути механічні редуктори, які не мають люфтів, електронні лампи та ін.
Аперіодична лавка першого порядку.її іноді називають інерційним, релаксаційним або одноємнісним елементом. Така ланка має рівняння динаміки
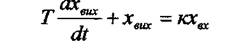
|
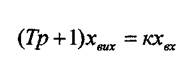
|
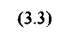
або в операторному вигляді
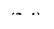
{ЗА)
Розв'язок такого лінійного неоднорідного диференціального рівняння першого порядку має вигляд
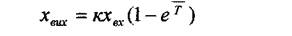
|

|
|
Відповідна часова характеристика - це експонента, зображена на рис. 5. і
(крива 1).
Якщо вхідна величина відсутня (що відповідає, наприклад, відключенню напруги з деякого активно - індуктивного опору), то динамічний процес можна записати у вигляді однорідного рівняння

яке називають рівнянням незбуреного руху. Розв'язок його має вигляд

Відповідна часова характеристика зображена на рис. 3.1 (крива 2). В усіх наведених вище рівняннях Т є стала часу, яка характеризує інерційні властивості відповідної ланки.
При наявності осцилограми вона може бути визначена при t = T. При цьому розв'язок матиме вигляд
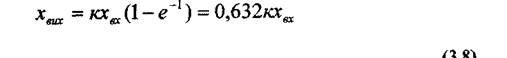
|
Відкладаючи по вертикальній осі 0,632 кх^ , легко знаходимо відповідне значення Г на осі часу і. Тривалість перехідного процесу t = (3 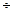 4 )Т. Якщо ланка має рівняння динаміки вигляду
4 )Т. Якщо ланка має рівняння динаміки вигляду

то її називають нестійкою аперіодичною ланкою. Розв'язок цього рівняння має вигляд
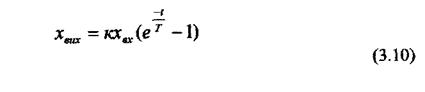
|
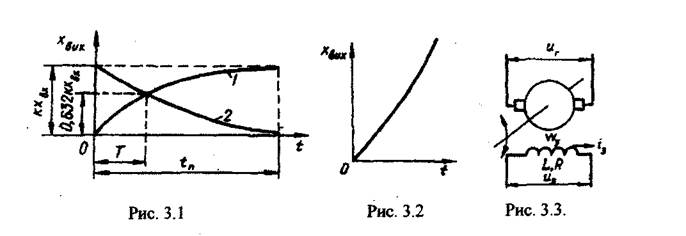
Часова характеристика ланки, зображена на рис. 3.2, показує, що при 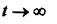
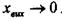
Аперіодичними ланками є різні електротехнічні пристрої з активно -індуктивним опором, механічні інерційні пристрої, генератори постійного струму таін.
Ланки другого порядку.До цієї групи відносять ланки, які мають рівняння динаміки вигляду

Позначивши 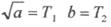 дістанемо рівняння в операторній формі запису
дістанемо рівняння в операторній формі запису
у вигляді
Розв'язок цього рівняння 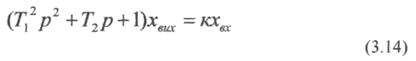
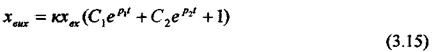
де 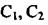 - сталі інтегрування;-
- сталі інтегрування;- 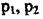 корені характеристичного рівняння.
корені характеристичного рівняння.
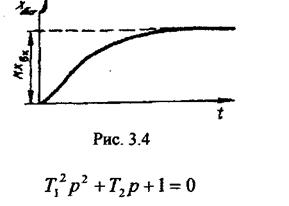
Залежно від коренів характеристичного рівняння можливі два різновиди
ланок другого порядку - аперіодичні та коливальні. Ці ланки мають один і той
самий зовнішній вигляд рівняння, але різко відрізняються по Рис, з 4 вигляду
часової характеристики.
Аперіодичні ланки другого порядку. До ланок цього виду відносять ланки при дійсних, від'ємних коренях характеристичного рівняння
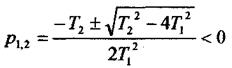
Це можливо за умови, коли 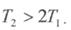
При 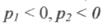 розв'язок рівняння ланки матиме вигляд
розв'язок рівняння ланки матиме вигляд
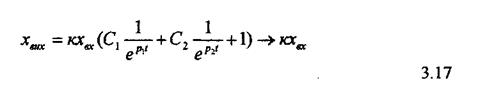
Часову характеристику наведено на рис. 3.4. Вона визначається сумою двох експонент, що і зумовлює назву ланки.
Коливальні ланки. Коливальною ланкою є елемент другого порядку при комплексних коренях характеристичного рівняння з від'ємною дійсною частиною.
В цьому випадку 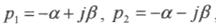 , де
, де
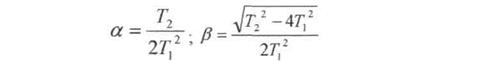
|
Розв'язок рівняння динаміки елемента можна записати у вигляді
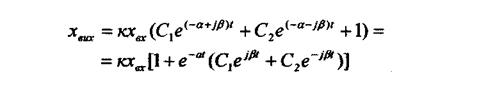
Згідно з формулою Ейлера
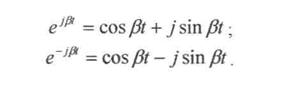
|
Замінюючи показникові функції на тригонометричні, після нескладних перетворень дістанемо
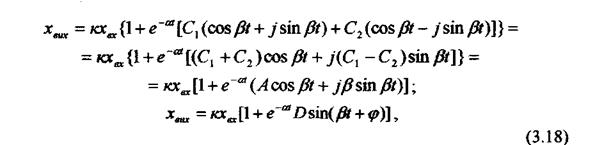
|
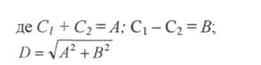
|
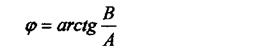
|
| - амплітуда гармонічних коливань; |
| - зсув по фазі. |
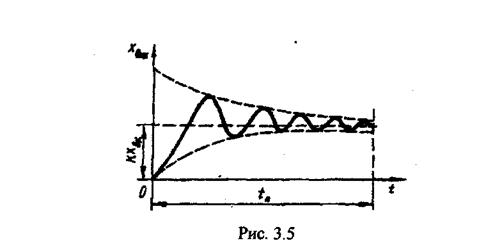
Часову характеристику, що відображує затухаючий коливальний процес і побудову згідно з рівнянням (3.18), наведено на рис. 3.5.
|
Тривалість перехідного процесу 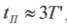 , де
, де 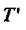 - стала часу апроксимуючої
- стала часу апроксимуючої
експоненти, показаної пунктиром, що залежить від дійсної складової комплексного кореня:
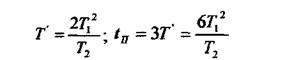
З наведеної формули видно, що коливальні властивості ланки другого порядку визначаються коефіцієнтом 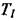 при другій похідній, а демпфуючі -коефіцієнтом
при другій похідній, а демпфуючі -коефіцієнтом 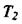 при першій похідній.
при першій похідній.
При Т2 <: 2Ті елемент другого порядку є коливальним, а при аперіодичним. 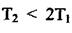
Рівняння ланки другого порядку можна записати також у дещо іншому вигляді
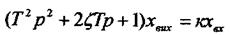
де 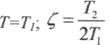 називають декрементом затухання.
називають декрементом затухання.
Залежно від величини 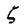 ланка другого порядку різко змінює свої
ланка другого порядку різко змінює свої
властивості. Згідно з цим, при 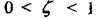 ланку називають коливальною. Цей
ланку називають коливальною. Цей
випадок детально розглянуто нами раніше.
Якщо 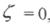 , ланку називають консервативною.
, ланку називають консервативною.
Часова характеристика даної ланки визначається розв'язком характеристичного рівняння, який при чисто уявних коренях матиме вигляд
або 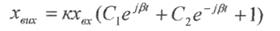
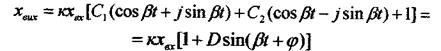
При цьому 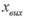 є коливанням із сталою амплітудою D при куті зсуву
є коливанням із сталою амплітудою D при куті зсуву
відносно початкової точки 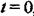 , що дорівнює
, що дорівнює 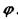
Ііри цьому хвих є коливанням із сталою амплітудою D при куті зсуву відносно початкової точки t = 0, що дорівнює 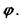
Прикладом елементів другого порядку можуть бути каскадні магнітні підсилювачі, електромеханічні підсилювачі поперечного поля та двигуни постійного струму.
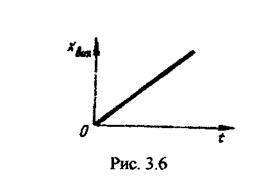
Інтегруючі (астатичні) ланки.Ланки даного типу мають рівняння динаміки вигляду

в операторній формі запису

|
|
Розв'язок цього рівняння має вигляд

Часову характеристику наведено на рис. 3.6. Вона показує, що при 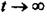
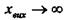 за умови, що на вході ланки існує вхідна величина і
за умови, що на вході ланки існує вхідна величина і 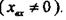
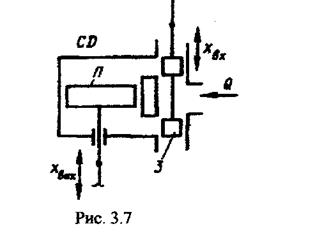
Прикладом інтегруючої (астатичної) ланки може бути гідравлічний серводвигун (рис. 3.7).
Вхідною величиною елемента. 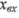 є переміщення золотника 3, а вихідною
є переміщення золотника 3, а вихідною 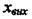 - переміщення поршня П. Рух поршня здійснюється за допомогою масла Q, яке надходить залежно від положення золотника у верхню або нижню порожнину
- переміщення поршня П. Рух поршня здійснюється за допомогою масла Q, яке надходить залежно від положення золотника у верхню або нижню порожнину
циліндра серводвигуна СД. Швидкість переміщення поршня 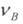 пропорційна
пропорційна
 |
кількості масла Q, що надходить у відповідну порожнину циліндра. Отже, можна записати
В свою чергу кількість масла в циліндрі пропорційна величині 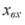 відхиленню золотника. Тому
відхиленню золотника. Тому 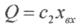 , звідки
, звідки 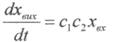
Інтегруючи праву і ліву частини рівняння, дістанемо
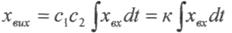
Диференціююча ланка.В ланках цього типу вихідна величина залежить від швидкості зміни вхідної. При сталому значенні вхідної величини вихідної величини не буде.
Рівняння динаміки елемента має вигляд
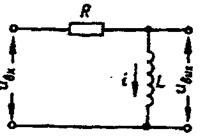
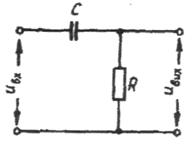
Рис. 3.8 Рис. 3.9
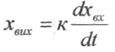
(3.24) або
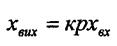 (3.25)
(3.25)
Прикладом елементів ланок даного типу можуть бути електричні кола L-R, R-C.
Ланки із запізненням.Характерними особливостями таких ланок є те, що величина, яка надходить на вхід, передається на вихід ланки з деяким запізненням 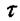 . У багатьох випадках приймають, що коефіцієнт передачі ланок із запізненням дорівнює одиниці. Прикладом таких елементів можуть бути трубопроводи, транспортери тощо.
. У багатьох випадках приймають, що коефіцієнт передачі ланок із запізненням дорівнює одиниці. Прикладом таких елементів можуть бути трубопроводи, транспортери тощо.
Рівняння ланок із запізненням мають вигляд
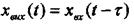 (3.28)
(3.28)
Після перетворень за Лапласом і використання теореми запізнення в ператорній формі запису рівняння матиме вигляд
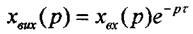 (3.29)
(3.29)
Крім розглянутих типових ланок, що відрізняються виглядом диференціальних рівнянь та значенням коренів характеристичного рівняння, можливі деякі інші підходи до класифікації ланок, які будуть розглядатися пізніше.
Години
Дата добавления: 2015-05-16; просмотров: 1477;
