Аналітичний опис елементів автоматики.

Щоб мати характеристики елементів автоматики, треба мати їх диференціальні рівняння. Найважче описувати регульовані об'єкти. В теорії систем автоматичного регулювання в основному застосовують чотири способи складання рівнянь динаміки.

Перший спосіб. Диференціальне рівняння складають аналітично на основі аналізу фізичних процесів, що відбуваються в елементі або

об'єкті.

Другий спосіб. Експериментальне визначають статичні і динамічні характеристики об'єкта або елемента. Зображують у вигляді графіка криву перехідного процесу, за якою визначають диференціальне рівняння.

Третій спосіб. На основі експерименту складають таблиці. Обробляють матеріал за допомогою регресійного аналізу.

Четвертий спосіб. Характеристики дістають на основі аналогового або цифрового моделювання елемента або об'єкта.

Крім того, комплексний коефіцієнт передачі визначають методом пасивного експерименту за спектральною густиною вихідних і вхідних випадкових стаціонарних процесів елемента або системи. Застосовують також методи, що ґрунтуються на подачі імпульсного і періодичного збурення.

Порядок диференціальних рівнянь залежить від складності процесів, що відбуваються в елементі, і від прийнятих допущень. Найкращі результати дає аналітичний опис регульованих об'єктів та елементів автоматики.

Як приклад розглянемо аналітичний опис дуже поширеного елемента автоматики - термопари, який перетворює теплову енергію в електричну.

В усталеному режимі температура робочого спаю 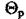дорівнює температурі середовища 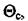яке оточує термопару. При рівновазі ЕРС термопари Е має певне значення, тому справедливий вираз

де k - сталий коефіцієнт.

Перенесемо миттєво термопару із зони з якоюсь незмінною температурою в зону з температурою 0_С. Кількість переданої за нескінченно малий відрізок часу й одержаної теплоти відповідно визначиться рівняннями:

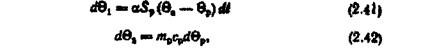
де 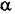- коефіцієнт тепловіддачі; S_p - площа поверхні робочого спаю; 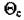температура середовища; 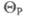- температура робочого спаю: 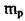- маса робочого спаю; с_р - питома теплоємність матеріалу робочого спаю; 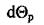- приріст

температури спаю при нагріванні протягом часу dt.

З умови рівності 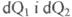можемо записати

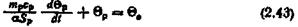
або, підставивши значення 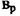із виразу (2.40),

Величини 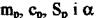- сталі для цієї термопари. Коефіцієнт передачі к має

розмір В/К. Визначимо розмір коефіцієнта при похідній

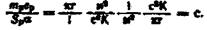
Отже, можна позначити

де Т - стала часу термопари.

Ураховуючи, що вхідною величиною термопари є температура середовища 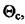а вихідною - ЕРС Е, то у загальному випадку рівняння термопари

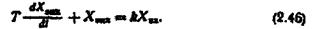
Розглянемо ще приклад аналітичного опису регульованого об'єкта з виконанням лінеаризації характеристики. Опишемо аналітичне повітряний ресивер (рис. 2.2). Припустимо, що на вході ресивера переріз труби становить 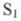а на виході 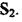Через переріз 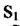у ресивер об'ємом V надходить газ під тиском 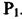Із ресивера газ через переріз 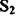іде до споживача під тиском 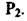При цьому в об'єкті встановлюється тиск разу Р. Перехідний процес в об'єкті можна описати рівнянням

де 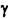- густина газу в ресивері; 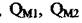- відповідно масові витрати, що

проходять через перерізи 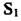і

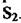
Якщо температура газу не змінюється, то рівняння (2.47) має вигляд

де R - газова стала; Т - абсолютна температура газу.

Масову витрату газу через переріз 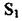можна визначити за формулою

де 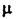- коефіцієнт витрати через переріз 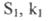- параметр, що є функцією від

показника адіабати.

Масову витрату газу через переріз 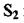визначимо за залежністю

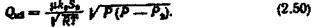
Підставимо (2.49) і (2.50) у рівняння (2.48) і дістанемо рівняння, яке описує динаміку об'єкта,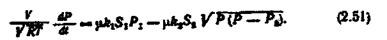

В усталеному режимі 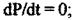отже,

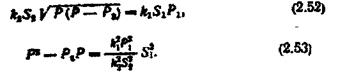
звідки після перетворення можна записати рівняння статики об'єкта

Тут вихідною величиною є переріз 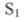заслінки, а вихідною - тиск газу в

об'єкті Р. Статична характеристика ресивера є істотно нелінійна (рис. 2.19, а).

Лінеаризуємо її в точці А, застосувавши залежність (2.8) до вихідного рівняння

(2.51) Тоді при незмінност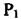і і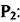

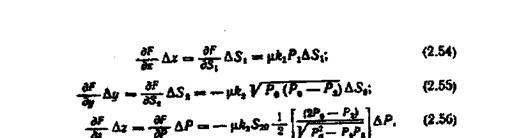
де 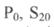- відповідно значення тиску Р в об'єкті і перерізу 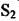в усталеному

режимі 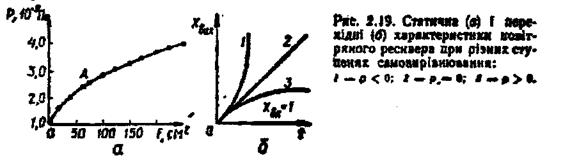в робочій точці.

З урахуванням добутих залежностей лінеаризоване рівняння у приростах матиме вигляд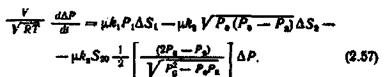

Статичної рівноваги регульованого об'єкта в робочій точці буде досягнуто при dp/dt=0 у рівнянні (2.51) і відповідних значеннях параметрів. Із цієї умови дістанемо масову витрату газу для усталеного режиму:

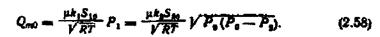
Поділимо ліву і праву частини рівняння (2.57) на 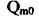і введемо відносні

змінні, враховуючи, що

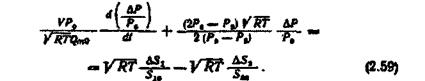
Поділивши ліву і праву частини рівняння (2.59) впишемо залежність у вигляді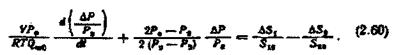

Визначимо розмір коефіцієнта при похідній

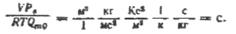
Отже можна позначити

де Т₀ - стала часу регульованого об'єкта. Введемо позначення:

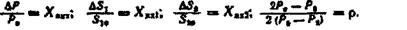
Запишемо рівняння об'єкта з урахуванням введених позначень

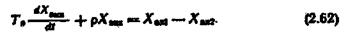
При S2=const матимемо

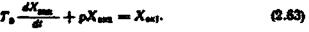
У добутому рівнянні змінні Хвих і Хвх є функціями часу.

Таким чином, дістали лінійне диференціальне рівняння, яке описує динамічні процеси в розглядуваному регульованому об'єкті. Параметр 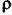у (2.63) є степенем самовирівнювання регульованого об'єкта Із введених позначень видно, що він не має розміру і є додатною величиною. Однак у режимах при 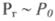може

досягати нескінченно великих і навіть від'ємних значень. Розглянемо поведінку об'єкта в усіх цих випадках.

Випадок L 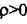. За рівнянням (2.63) зображення вихідної величини запишемо у вигляді

Досліджувати об'єкт будемо при одиничному вхідному діянні, що відповідає 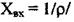З урахуванням цього

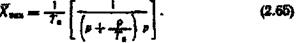
Розкладемо дріб у квадратних дужках на елементарні дроби і дістанемо

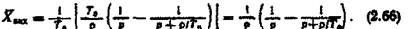
Здійснивши зворотний перехід, дістанемо

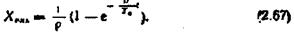
Випадок 2. 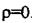За рівнянням (2.63) зображення вихідної величини матиме

вигляд

З урахуванням 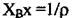дістанемо

Здійснивши зворотний перехід, запишемо рівняння

Випадок 3. 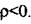Зображення вихідної величини при від'ємному значенні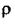

або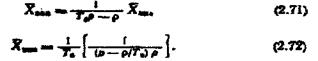

Розклавши дріб у квадратних дужках на елементарні дроби, дістанемо

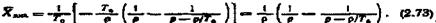
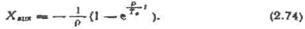
Рівняння (2.71) розв'яжемо, здійснивши зворотний перехід від зображення (2.73) до оригіналу:

Перехідні характеристики ресивера як регульованого об'єкта при різних степенях самовирівнювання, побудовані за залежностями (2.67), (2.70) і (2.74), показані на рис. 2.19, б. При р<0 (крива 1) об'єкт має від'ємне самовирівнювання. Якщо 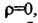об'єкт має нульове самовирівнювання (крива 2). У цих двох випадках

стійку роботу регульованого об'єкта без регулятора забезпечити неможливо. Об'єкт матиме додатне самовирівнювання, коли р>0 (крива 3). Переміщення заслінки на вході на певну величину забезпечить поступове зростання або спад тиску до заданого значення Р₀.

2. Здобуття статичних і динамічних характеристик систем автоматичного регулювання.

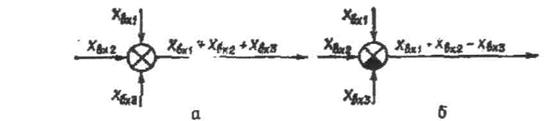
Ряс. 2.20. Елемент підсумовування (а) і порівняння (б)

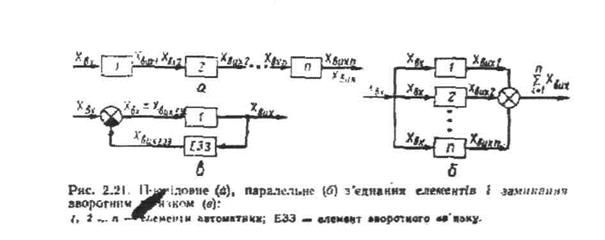
Відомі властивості окремих елементів дають змогу визначати статичні й динамічні характеристики всієї системи автоматичного регулювання, розглядаючи і змінюючи її структуру. Структурні компонування CAP здійснюють трьома способами з'єднання елементів між собою - послідовним, паралельним і замиканням зворотного зв'язку Сигнали на вході і виході окремих елементів додають або віднімають, застосовуючи відповідно підсумовуючі пристрої та елементи порівняння (рис. 2.20). Послідовне з'єднання (рис. 2.21, а) характеризується тим, що вихідна величина попереднього елемента є вхідною для наступного. У паралельному з'єднанні (рис. 2.21, б) на вхід усіх елементів подають одну й ту саму величину Х_вх. Вихідна величина дорівнює сумі вихідних сигналів усіх елементів. При замиканні зворотним зв'язком (рис. 2.21, в) вихідна величина Х_вих, пройшовши через елемент зворотного зв'язку ЕЗЗ, надходить на вхід елемента, додаючись до вхідного сигналу або віднімаючись від нього. Дуже часто в системах здійснюють пряму подачу вихідного сигналу на вхід. Такий зворотний зв'язок називають одиничним. Зворотні зв'язки можуть бути додатними й від'ємними, жорсткими і гнучкими, зовнішніми і внутрішніми. Елемент 1 у схемах може вважатися як окремим пристроєм, так і складним їх з'єднанням, що мають і зворотні зв'язки.

За відомими статичними характеристиками елементів і способом їх з'єднання будують результуючі статичні характеристики систем автоматичного регулювання. Статичні характеристики елементів задають аналітичне або графічно. Для лінійних елементів результуючу статичну характеристику можна знайти аналітичне, використовуючи розглянуті властивості з'єднань (рис. 2.21). Універсальним є графічний спосіб побудови результуючих характеристик CAP.

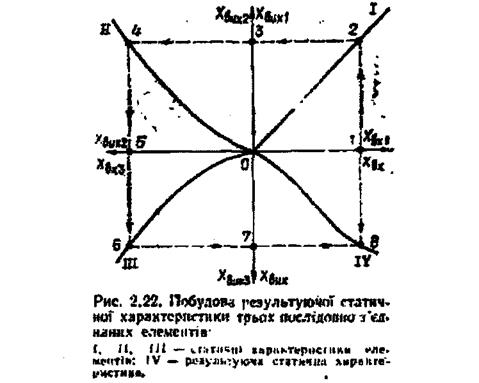
Методика побудови результуючої статичної характеристика трьох послідовно з'єднаних елементів показана на рис. 2.22. У декартовій системі координат будуємо характеристики І, II та III. Беремо вхідну величину (точка 1) і, враховуючи, що при послідовному з'єднанні вихідна величина попереднього елемента є вхідною для наступного, здійснюємо побудову відповідно до рисунка. Точку 8 результуючої характеристики IV дістаємо в останньому квадранті. Виконавши низку таких побудов, дістаємо результуючу характеристику послідовного з'єднання. При великій кількості елементів побудову здійснюємо в інших квадрантах, на одній осі відкладаючи вхідну, а на другій - вихідну величину.

При паралельному з'єднанні (рис. 2.23) усі характеристики будуємо в одному квадранті. Беремо вхідну величину (точка l) і з огляду на те, що при паралельному з'єднанні вхідна величина спільна для всіх, елементів, визначаємо ординати (2, З, 4). Підсумовуючи ординати, дістаємо точку 5, що належить результуючій характеристиці. Повторивши низку побудов, дістаємо результуючу характеристику IV Побудову легко виконати для будь-якої кількості елементів.

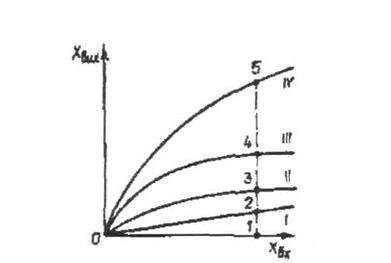
Рис.2.23, Побудоварезультуючої статичної характеристики трьох паралельно з'єднаних елементів:I, II, III — характеристикиелементів: IV — результуюча характеристика

Побудова статичної характеристики з'єднання при замиканні зворотним зв'язком показана на рис. 2.24, На кресленні наносимо характеристики з'єднання І, що замикається зворотним зв'язком, і елемента зворотного зв'язку П. Беремо вхідну величину (рис. 224, а, точка 1) і визначаємо вихідну величину елемента зворотного зв'язку (точка 5). Оскільки при замиканні від'ємним зворотним зв'язком сигнали на вході з'єднання віднімаються, наносимо точку 8, що відповідає результуючому значенню вхідної величини, їй відповідатиме вихідний сигнал, що визначається за характеристикою І. Цей вихідний сигнал при поданому вхідному визначає точку 10 на результуючій характеристиці Ш з'єднання. При додатному зворотному зв'язку вхідний сигнал збільшують (рис, 2.24, б, точка 8). Виконавши потрібну кількість побудов, дістаємо результуючу характеристику Ш.

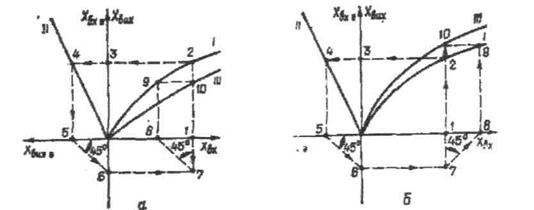
Рис. 2.24. Побудова результуючої статичної характеристики при заміненні негативним (а) і позитивним (б) зворотними зв'язками: