Умови стійкості систем автоматичного регулювання.

Вихідна величина виведеної з рівноваги системи автоматичного регулювання в результаті здійснюваних рухів може точно або з деякою похибкою повернутись до попереднього значення, безмежно відхилятися від заданого значення або здійснювати незатухаючі коливання.

Характер поведінки систему в перехідному режимі визначається диференційним рівнянням

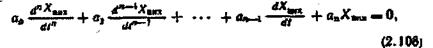
яке утворюється з характеристичного рівняння (2.107).

Якщо вихідна величина 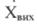здійснює незатухаючі коливання або безмежно відхиляється від заданого значення, така лінійна система нестійка і, природно, непрацездатна. В стійкій системі відхилення вихідної величини від заданого значення з перебігом часу від початку перехідного процесу має прямувати до нуля або до якоїсь сталої величини. Вихідна величина при цьому приходить до заданого значення або відрізняється від нього в межах статичної помилки Зрозуміло, що працездатні лише стійкі системи, тому при розробці системи автоматичного регулювання її завжди треба перевіряти на стійкість. Висновок про стійкість системи можна зробити, визначивши після розв'язання рівняння (2.108) відхилення X регульованої величини 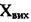від заданого значення в часі £ Система буде стійкою, якщо відхилення X прямуватиме до нуля або до певної сталої при 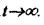Як відомо,

загальним розв'язанням рівняння (2.108) буде

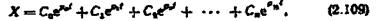
де 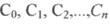- сталі;- 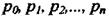корені характеристичного рівняння

(2.107).

Для стійкості системи треба, щоб кожен член правої частини рівняння (2.109), починаючи з другого, з перебігом часу прямував до нуля. Неважко побачити, що це можливо тільки при від'ємних значеннях коренів 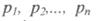характеристичного рівняння системи. Якщо корені від'ємні, кожен член рівняння з перебігом часу прямуватиме по експоненті до нуля, і відхилення регульованої величини від заданого значення дорівнюватиме сталій С₀ при 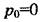або нулю при

С₀=0. Якщо хоча б один корінь буде додатним, з перебігом часу X необмежено зростатиме.

При комплексних коренях характеристичного рівняння, що можливо при певних параметрах елементів системи, кожен із розглядуваних членів рівняння (2.109) зображуватиме коливальну криву, яка сходиться при від'ємній дійсній частині кореня і розходиться при додатній дійсній частині кореня.

Отже, лінійна система автоматичного регулювання буде стійкою, якщо всі дійсні корені і всі дійсні частини комплексних коренів характеристичного рівняння будуть від'ємними. Якщо корені характеристичного рівняння нанести на комплексну площину, то система автоматичного регулювання буде стійкою при розташуванні всіх коренів ліворуч від уявної осі.

Знаки дійсної частини коренів можна знайти безпосереднім розв'язуванням характеристичного рівняння. Однак легко розв'язуються рівняння не вище другого

ступеня. Рівняння третього і четвертого ступенів аналітичне розв'язуються надзвичайно складно, а рівняння вищих ступенів взагалі не можуть бути розв'язані в радикалах.

Для полегшення дослідження систем на стійкість запропоновано непрямі методи визначення знака дійсної частини коренів характеристичного рівняння, які дістали назву критеріїв стійкості. Ці методи не передбачають розв'язання характеристичного рівняння.

Розрізняють алгебраїчні і частотні критерії стійкості. До алгебраїчних належать критерій Вишнєградського (1876 р.), Рауса (1877 p.) і Гурвіца (1895 p.). До частотних належать критерій Найквіста (1932 р.), Михайлова (1938 p.), Найквіста - Михайлова (1938 p.), а також метод логарифмічних частотних характеристик. Далі розглянемо тільки ті критерії стійкості, які найбільше використовують на практиці.

Поряд із критеріями застосовують необхідну (але недостатню) умову стійкості Стодоли, згідно з якою для стійкої системи потрібно, щоб усі коефіцієнти характеристичного рівняння мали однакові знаки. Через недостатність умови при однакових знаках коефіцієнтів корені характеристичного рівняння можуть мати додатний знак, тому потрібна перевірка стійкості. Однак, якщо знаки коефіцієнтів різні, або хоча б один корінь характеристичного рівняння буде додатним, то система буде нестійкою. Таким чином, умова Стодоли дає змогу за видом характеристичного рівняння визначити нестійку систему.

Критерії стійкості дають змогу тільки встановити факт стійкості системи. Особливе місце в теорії лінійних систем посідають методи виділення ділянок стійкості, одну з яких буде розглянуто далі.

2. Критерій стійкості Гурвіца.

Критерій стійкості Гурвіца дає змогу визначати стійкість систем автоматичного регулювання досить високого порядку, але користуватися цим критерієм порівняно легко лише при рівняннях до п'ятого порядку, оскільки надалі значно зростає складність обчислень.

Для визначення стійкості системи треба з коефіцієнтів характеристичного рівняння

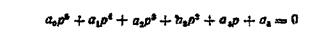
скласти визначники й обчислити їх. Визначники складають при а₀ >0, тому, якщо треба, характеристичне рівняння множать на -1.

Система буде стійкою при всіх додатних визначниках:

* _ *

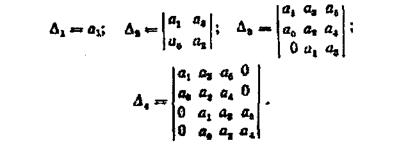
У кожному визначнику кількість рядків дорівнює кількості колонок і номеру визначника. По головній діагоналі вписують коефіцієнти від а₀ до коефіцієнта з номером, який дорівнює номеру визначника. Колонки від елементів головної діагоналі вгору доповнюють коефіцієнтами з послідовно зростаючими індексами,

униз - з убуваючими індексами. На місці відсутніх коефіцієнтів, індекси яких більші п і менші 0, проставляють нулі.

Як видно, кількість визначників на одиницю менша від порядку характеристичного рівняння. Отже, для системи четвертого порядку треба скласти три перших визначники, системи третього порядку - два, другого - один визначник.