Визначення стійкості систем автоматичного регулювання.
Визначення стійкості систем автоматичного регулювання розглянемо на прикладі астатичної CAP, що має рівняння (2.101). Нехай параметри динамічних ланок дорівнюватимуть: 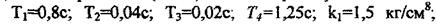
 Після підставляння числових значень параметрів динамічних ланок дістанемо коефіцієнти характеристичного рівняння (2.101) системи:
Після підставляння числових значень параметрів динамічних ланок дістанемо коефіцієнти характеристичного рівняння (2.101) системи:
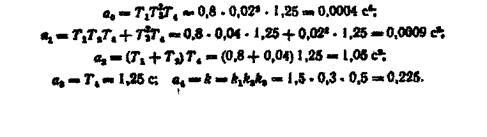
Характеристичне рівняння системи матиме вигляд
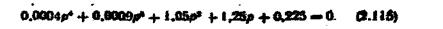
Приклад. Перевіримо на стійкість за допомогою критерію Гурвіца систему автоматичного регулювання, що описується рівнянням (2,115).
Для системи четвертого порядку треба скласти три визначники:
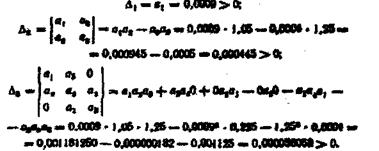
|
Усі визначники додатні, току система стійка.
Приклад. Перевіримо на стійкість за допомогою критерію Михайлова систему з характеристичним рівнянням (2.115). Підставимо у рівняння замість 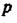 уявне число
уявне число 
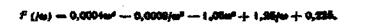
Відокремимо дійсну й уявну частини:
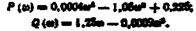
Підставляючи значення  дістанемо координати точок
дістанемо координати точок
годографа, округлені значення яких наведено в табл. 2.1. Із даних таблиці видно, що годограф, не заходячи в початок координат, на комплексній площині проти годинникової стрілки проходить через чотири квадранти, що відповідає стійкій системі четвертого порядку.
При перетині годографом початку, координат система міститься на граниш стійкості. Це можливо при збільшенні коефіцієнта підсилення системи до критичного значення. Прирівняємо до нуля 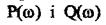 і визначимо значення
і визначимо значення
критичного коефіцієнта підсилення системи. Із рівняння 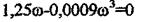 знаходимо частоту, що дорівнює
знаходимо частоту, що дорівнює 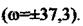 Підставимо знайдене значення частоти
Підставимо знайдене значення частоти
у рівняння 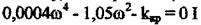 знайдемо
знайдемо 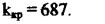
Приклад. Перевіримо на стійкість за допомогою критерію Найквіста -Михайлова астатичну систему, що має передаточну функцію (2.99).
2.1. Координати точок годографа Михайлова

2.2. Дані для побудови амплітудно-фазової частотної характеристики
розімкнутої системи

2.3. Дані для побудови кривої D-розбитгя

|
Передаточна функція розімкнутої системи
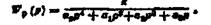
З урахуванням прийнятих значень параметрів
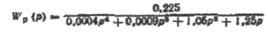
Підставимо 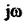 замість оператора р і дістанемо математичний вираз комплексного передаточного коефіцієнта розімкнутої системи:
замість оператора р і дістанемо математичний вираз комплексного передаточного коефіцієнта розімкнутої системи:
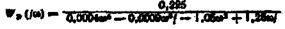
Помножимо чисельник і знаменник 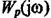 на сполучений із знаменником
на сполучений із знаменником
вираз і відокремимо дійсну й уявну частини:
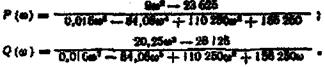
Підставляємо у ці вирази значення частоти від 0 до 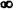 й обчислюємо
й обчислюємо 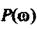 і
і
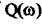 [табл.
[табл.  2.2].
2.2].
Підставимо у церівняння 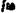 замість
замість 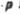 і дістанемо
і дістанемо
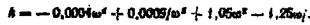
Відокремимо дійсну й уявну частини
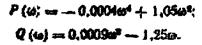
За даними табл. 2.2 на комплексній площині будуємо амплітудно-фазову характеристику розімкнутої системи (рис. 2.34). Оскільки крива не охоплює точку з координатами 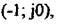 система стійка.
система стійка.
Приклад. Виділити ділянку стійкості за коефіцієнтом підсилення астатичної системи, що описується рівнянням (2.101),
Змінюючи частоту від 0 до 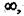 знайдемо значення
знайдемо значення  і
і  кривої
кривої
D-розбиття, які занесемо до табл. 2.3. Враховуючи, що при зміні частоти від 0 до - 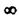 дістанемо ті самі значення
дістанемо ті самі значення 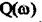 зі зворотнім знаком, за даними табл. 2.3
зі зворотнім знаком, за даними табл. 2.3
побудуємо криву D-розбиття (рис. 2.35). Штриховка показує, що ділянка І є імовірною ділянкою стійкості. Перевірка системи на стійкість при 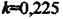 показує,
показує,
що ділянка І є ділянкою стійкості. Ділянка стійкості підтверджує, що критичний коефіцієнт підсилення цієї системи становить 687. Це також було доведено критерієм стійкості Михайлова.
Години
Дата добавления: 2015-05-16; просмотров: 1390;
