Критерій стійкості Найквіста- Михайлова.

Спершу критерій розробив у 1932 р. X. Найквіст стосовно електронних підсилювачів із зворотним зв'язком, а в 1938 р. А. В. Михайлов поширив цей критерій на снетеми автоматичного регулювання. За цим критерієм стійкість замкнутої системи автоматичного регулювання визначають за амплітудно-фазовою характеристикою стійкої розімкнутої системи. Розімкнута система автоматичного регулювання стійка в тому разі, коли складається тільки із стійких динамічних ланок і має не більше однієї інтегруючої ланки. Цей критерій з іншим

формулюванням також можна застосовувати для дослідження систем, що містять як інтегруючі (нейтральні), так і нестійкі ланки [13].

Амплітудно-фазову характеристику розімкнутої системи дістають так. Розривають лінію зовнішнього зворотного зв'язку системи на структурній схемі й аналізують динамічні ланки, що входять до головного контуру. Якщо головний контур системи не містить нестійких ланок і має не більше однієї інтегруючої ланки, можна застосовувати критерій стійкості Найквіста - Михайлова. За структурною схемою розімкнутої стійкої системи визначають передаточну функцію. Підставивши замість оператора р добуток 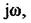дістають рівняння

амплітудно-фазової характеристики розімкнутої системи, праву частину якого зображують у вигляді дійсної 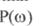й уявної складових, то залежать від

частоти. Змінюючи частоту w від 0 до дістають пари значень 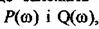за

якими на комплексній площині будують амплітудно-фазову характеристику стійкої розімкнутої системи.

Якщо ця характеристика не охоплює точку з координатами 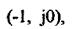то

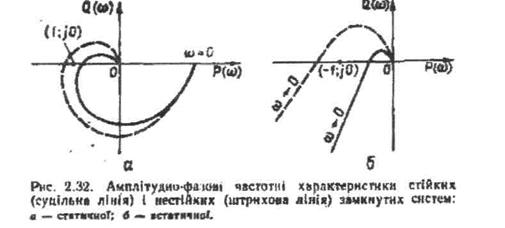
замкнута система автоматичного регулювання стійка. На рис. 2.32 показані амплітудно-фазові характеристики стійких і нестійких замкнутих статичної (рис. 2.32, а) й астатичної (рис. 2.32, б) систем. Збільшення коефіцієнта підсилення розімкнутої системи спричинює зростання модуля амплітудно-фазової характеристики. При певному його значенні, яке називається критичним, амплітудно-фазова характеристика пройде через точку 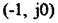і система буде на

гранці стійкості. Якщо 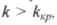система втратить стійкість. Віддаляння амплітудно-

фазової характеристики від точки 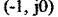визначає запас стійкості за фазою і за

амплітудою h (рис. 2.32, а).

При визначенні стійкості систем користуються логарифмічними амплітудною і фазовою частотними характеристиками розімкнутої системи. Очевидно, замкнута система автоматичного регулювання буде стійкою, якщо частота 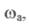при якій логарифмічна амплітудна частотна характеристика перетинає вісь абсцис, менша від частоти w_зр при якій логарифмічна фазова частотна характеристика перетинає лінію 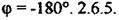Виділення ділянок стійкості

Розглянуті вище критерії дають змогу визначити, чи стійка система автоматичного регулювання при певних параметрах її елементів. Практично критерії не дають відповіді на питання про границі зміни того чи іншого параметра системи при умові збереження або досягнення стійкості. Границі або ділянку зміни одного або кількох параметрів системи можна знайти за допомогою спеціального методу, що дістав назву D-розбиття.

Вперше завдання виділення ділянок стійкості для систем третього порядку розв'язав І. А. Вишнєградський. У 1947 р. Д. Неймарк розв'язав це завдання для систем, що описуються диференціальними рівняннями будь-якого порядку. Метод D-розбиття за двома дійсними параметрами потребує трудомістких обчислень, тому його застосовують рідко. Розглянемо простіший метод D-розбиття за одним комплексним параметром на прикладі астатичної системи автоматичного регулювання тиску повітря в резервуарі, яка описується рівнянням (2.101). Характеристичне рівняння системи матиме вигляд

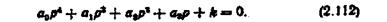
Припустимо, що в рівнянні (2.112) усі коефіцієнти відомі і незмінні, крім, наприклад, коефіцієнта підсилення 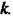Нехай при якомусь значенні коефіцієнта підсилення два корені характеристичного рівняння містяться в лівій півплощині на комплексній площині, а два - в правій півплощині. Два корені мають додатні дійсні частини, отже, система нестійка.

З огляду на неперервну залежність між коефіцієнтами алгебраїчного рівняння і значенням його коренів можна, змінюючи коефіцієнт к, наблизити корені, що містяться в правій півплощині, до уявної осі, розташувати їх на уявній осі і перевести в іншу півплощину. Перші два корені за певних умов можуть не виходити з лівої півплощини, і система стане стійкою. Змінюючи значення коефіцієнта підсилення можна переміщувати корені в лівій півплощині, і система залишатиметься стійкою. На комплексній площині коефіцієнта підсилення 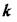(робимо припущення про його комплексність) можна виділити ділянку значень цього параметра, при яких система стійка. Це й є ділянка стійкості. При значеннях коефіцієнта підсилення 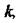що лежать поза цією ділянкою, система втратить стійкість. Границею ділянки стійкості є значення коефіцієнта підсилення системи 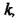при яких хоча б один корінь міститься на уявній осі. Таким чином, границею стійкості є відображення уявної осі комплексної площини коренів характеристичного рівняння на комплексній площині коефіцієнта

Аналогічно можна міркувати про будь-який із коефіцієнтів характеристичного рівняння системи, проте на практиці такий підхід пошуку ділянок стійкості не використовують. Набагато зручніше користуватися конкретними параметрами динамічних ланок - сталими часу й коефіцієнтами підсилення, які до рівняння (2.112) входять лінійно і їх можна легко змінювати. Такими параметрами в розглядуваній системі можуть бути коефіцієнт підсилення важільного підсилювача і стала часу виконавчого механізму Стала часу 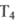входить до всіх коефіцієнтів характеристичного рівняння (2.112), а коефіцієнт 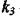до коефіцієнта підсилення системи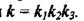

Припустимо, що в рівнянні (2.112) усі коефіцієнти відомі, за винятком 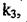який позначимо в загальному випадку через 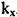. Визначимо з рівняння (2.112) шуканий параметр

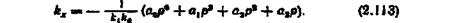
Підставивши у рівняння (2.113) замість р уявне число jco і відокремивши дійсну й уявну частини, дістанемо

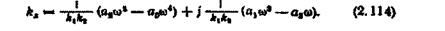
Рівняння (2.114) при зміні w від 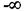до 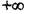дає змогу дістати значення 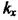для всіх можливих коренів, розташованих на уявній осі. Природно, що значень решти трьох коренів у кожному обчисленні при 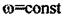ми не знаємо. Діставши для

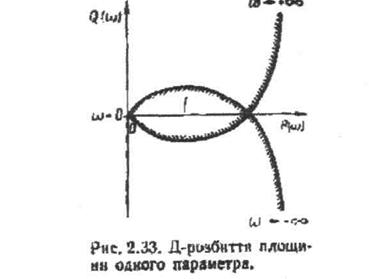
різних w пари значень дійсної Р((а) й уявної Q(cu) складових, будуємо на комплексній площині параметра к_х криву, що є відображенням уявної осі комплексної площини коренів характеристичного рівняння (рис. 2.33),

Оскільки у стійкій системі всі корені містяться ліворуч від уявної осі, при обході її від 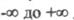ділянка стійкості також буде ліворуч від добутої кривої. Для

зручності відшукання ділянки стійкості нанесемо на криву (рис. 2.33) штриховку зліва при русі від 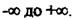Ділянка І на рис, 2.33, можливо, є ділянкою стійкості.

Узявши будь-яке дійсне значення усередині добутої ділянки,

обчислюємо коефіцієнти Підставляючи значення 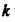у рівняння (2.112), за

допомогою будь-якого критерію стійкості перевіряємо стійкість системи. Якщо система виявиться стійкою, відшукана ділянка є ділянкою стійкості. Ця перевірка потрібна тому, що при певному значенні 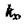яке лежить на границі ділянки стійкості, крім уявного кореня, коренів з від'ємною дійсною частиною могли бути корені і з додатною дійсною частиною. Може трапитись, що ділянка стійкості немає, і система, отже, нестійка при будь-якому значенні 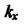або іншому розглядуваному параметрі. Якщо ділянки стійкості немає, система автоматичного регулювання називається структурно-нестійкою. Щоб добитися стійкості цих систем, треба змінити структурну схему - ввести додаткові, замінити одну або кілька ланок або змінити порядок з'єднання елементів. У структурно-стійких системах для досягнення стійкості треба тільки змінити числові значення параметрів.