І - характеристика елемента, що охоплюється: ІI — елемента зворотнього зв`язку: III — результуюча.

Відповідно до розглянутих правил дістають результуючі характеристики замкнутих систем автоматичного регулювання.

Динамічні характеристики звичайно дістають за передаточними, функціями систем, що визначаються з використанням способу з'єднання елементів і таких залежностей.

При послідовному з'єднанні елементів

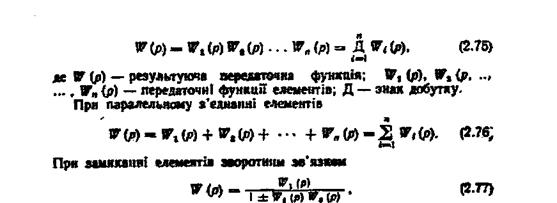
де Wi(p) і Wo(p) - відповідно передаванні функції з'єднання, що охоплюється зворотним зв'язком, і колом зворотного зв'язку. Якщо зворотний зв'язок від'ємний, ставлять знак плюс, при додатному - мінус.

Використовуючи залежності (2.75)-(2.77), можна CAP будь-якої структурної складності звести до якогось узагальненого елемента, охопленого зовнішнім зворотним зв'язком, який з'єднує вихід системи зі входом. Передаточну функцію узагальненого елемента називають передаточною функцією розімкнутої системи W_p(p). З урахуванням зворотного зв'язку можна дістати передаточну функцію замкнутої системи W (р) за залежністю (2.77)

Звичайно зовнішній зворотний зв'язок завжди одиничний, тобто Wo(p)=l. З урахуванням цього передаточна функція замкнутої системи

Вихідна (регульована) величина системи завжди одна й та сама. Вхідні величини можна брати різними. У зв'язку з цим можна розглядати різні передаточні функції систем Найчастіше визначають передаточні функції за допомогою керуючого діяння, проте можна мати й передаточні функції за задавальним діянням і за помилкою.

За допомогою результуючих передаточних функцій W_p (p) і W₃ (p) можна за розглянутою раніше методикою дістати всі необхідні характеристики систем. Багато які з них при побудові відзначаються трудомісткістю, що потребує застосування наближених методів. Результуючу логарифмічну амплітудну частотну характеристику розімкнутої одноконтурної системи можна будувати, користуючись наближеним способом.

Передаточну функцію розімкнутої одноконтурної системи можна записати у вигляді

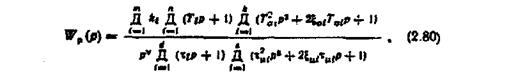
де v - порядок астатизму (кількість інтегруючих ланок). Прологарифмувавши цей вираз після підставляння 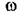замість р і перетворення, неважко пересвідчитись, що ЛАЧХ одноконтурної системи можна дістати підсумовуванням ординат ЛАЧХ окремих, що входять до CAP, елементів.

При цьому визначають сполучні частоти 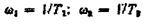і т. д. і наносять

їх на осі частот. Проводять низькочастотну асимптоту, яка при 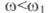є прямою з

нахилом 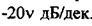Ця пряма при повинна 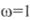мати ординату -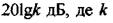

коефіцієнт підсилення розімкнутої системи. Після кожної із сполучних частот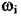

змінюють нахил характеристики 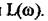Якщо сполучна частота належить елементу з

передаточною функцією 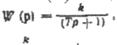нахил змінюють на 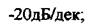на

-40дБ/дек при 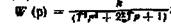'на +20дБ/дек при 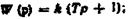на

-40дБ/дек при 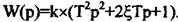При високих частотах (більших від

найвищої сполучної частоти) асимптота ЛАЧХ повинна мати нахил -20 :,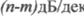

де 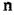- порядок знаменника; 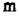- порядок чисельника передаточної функції W_p(p), враховуючи добуток співмножників чисельника і знаменника.

Логарифмічну фазову частотну характеристику розімкнутої одноконтурної системи дістають також в результаті простого додавання ординат ЛФЧХ окремих елементів, що входять до системи.

Годин