Уравнений методом Ньютона
Запишем нелинейную систему уравнений в общем виде
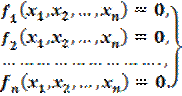(2.24)
Эту систему можно записать короче в матричном виде, рассматривая совокупность аргументов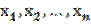 
как n-мерный вектор:
х =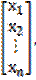 
а совокупность функций f1, f2 ,…, fn – тоже как n-мерный вектор:
f =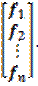 
Тогда будем иметь
f(х) = 0.(2.25)
Для решения системы (2.24) будем пользоваться методом последовательных приближений. Предположим, что найдено р-е приближение
х(р) = ( 
)одного из корней х = (х1, х2, …, хn)векторного уравнения (2.25). Тогда точный корень уравнения можно представить в виде
х = х(р) + ε(р) = 0,(2.26)
где ε(р) = (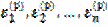 
) – погрешность корня. Подставляя выражение (2.26) в уравнение (2.25), будем иметь
f (х(р) + ε(р)) = 0.(2.27)
Предполагая, что функция f(х)непрерывна, и дифференцируема, разложим левую часть уравнения (2.27) по степеням малого вектора ε(р), ограничиваясь линейными членами
f(х(р) + ε(р)) = f(х(р))+ f’(х(р)) ε(р) = 0,(2.28)
где f’(x)есть матрица Якоби системы функций f1, f2,…, fn относительно переменных х1, х2,…, хn, т.е.
f’(x) = W(x) =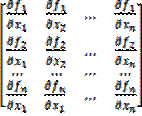 
Учитывая эту матрицу, формулу (2.28) можно записать в виде
f(х(р)) + W(х(р))ε(p) = 0.
Отсюда, предполагая, что матрица W(х(р))неособенная (ее определитель не равен 0), получим
W(х(р)) ε(p) = - f(х(р))
По аналогии с методом касательных, где (n+1) – е приближение выражается через формулу (2.4), (р+1)–е приближение в нашем случае можно записать в виде
х(р+1) = x(p) – W-1(x(p))f(x(p)), p = 0,1,2,…(2.29)
За нулевое приближение х(0)можно взять грубые значения искомого корня.
Пример. Методом Ньютона найти приближенное решение системы уравнений
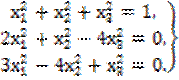
За начальное приближение примем следующие значения неизвестных: х0 = у0 = z0 = 0,5.
Дата добавления: 2015-02-03; просмотров: 924;