Интерполяционная формула Лагранжа
Для получения интерполяционной формулы Лагранжа мы будем исходить из понятия параболического интерполирования. Рассмотрим функцию f(x), для которой заданы значения уi = f(xi), i = 0, 1, 2,…, n, причем все хiуiизвестны. Требуется определить многочлен у = F(x) степени n, для которою F(xi) =f(xi).
Искомый многочлен можно записать в виде
F(x) = a0 + a1x1 + a2 
+ … + an 
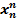(3.3
Чтобы отыскать неизвестные коэффициенты a0, a1,..., an, используя приведенные выше условия, можно написать систему из (n+1) уравнений с(n+1) неизвестными. Эта система будет иметь следующий вид:
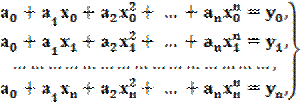. (3.4)
Вместо того, чтобы решать систему уравнений (3.4), можно поступить иначе: непосредственно построить многочленF(x), удовлетворяющий всем поставленным условиям.
Найдем прежде всего выражение для многочлена, принимающего в точке х = х0 значение у0 = 1, а в точках х = х1, х = х2 ,…,х = хn – значения у1 = у2 = ... = уп = 0. Можно проверить, что такой многочлен будет иметь следующий вид:
.
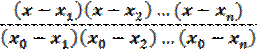Действительно, значения х = х1, х = х2 ,…, х = хnявляются корнями этого многочлена, а при х = х0 числитель равен знаменателю.
Теперь построим многочлен у= F0(x), принимающий в точке х = x0 значение y0 и обращающийся в нуль для значений x = xi (i = 0, 1, 2, ..., n). Учитывая предыдущее построение, нетрудно заметить, что многочленF0(x) должен иметь вид
После этих предварительных построений можно перейти к отысканию многочлена F(x), принимающего в точках x = xi (i = 0,1,2,...,n) заданные значенияF(xi) = уi..Для этого определим при фиксированном индексе j (0 ≤ j ≤ n) многочленFj(x),принимающий в точке x = хj значениеFj(xj) = yj = F(xj), а во всех остальных точкахx = xi (i = 0, 1, 2, ..., n, i ≠ j) значения F2(xi)=0. Очевидно, это будет многочлен
Fj(x) =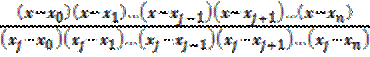 
yj.
Искомый многочлен будет равен сумме
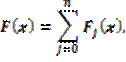
так как в каждой точке хj только одно из слагаемых принимает нужное значение yj, а все остальные слагаемые обращаются в нуль. Итак, искомый многочлен найден. Подставляя в сумму вместо Fj(x) их выражения, получим
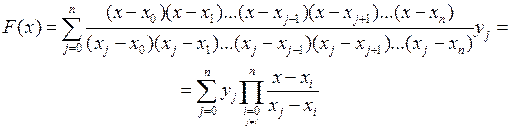(3.5) 
В развернутом виде выражение (3.5) имеет вид
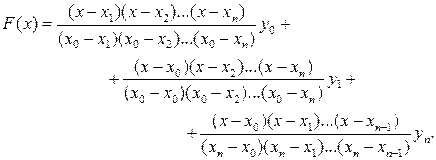(3.6)
Полученная формула (3.6) называется интерполяционной формулой Лагранжа.
Рассмотрим примеры. Положим п=1. В этом случае мы имеем две точки х0 и х1, и формула Лагранжа дает уравнение прямой. Обозначив абсциссы этих точек х0=а и х1=b, получим интерполяционный многочлен в виде
F(x) =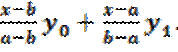 
Теперь положим n=2. Тогда мы получим уравнение параболы, проходящей через три точки. Абсциссы этих точек обозначим х0 = а, х1 = b,
х2 = с. Тогда искомое уравнение будет иметь вид
F(x) =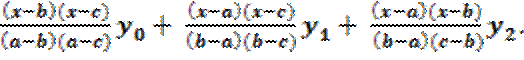 
Дата добавления: 2015-02-03; просмотров: 1238;