Вариационный метод Лагранжа.




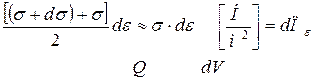
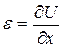 - безразмерная величина
- безразмерная величина
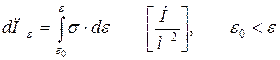
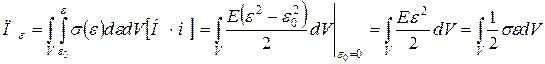
В трехмерном случае:
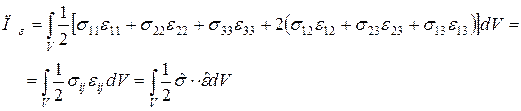
Элементарная работа внутренних сил:
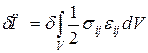
Здесь δ – кинематически допустимая вариация, т.е. произвольно изменяется поле перемещений на бесконечно малую величину 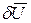 , причем кинематические краевые условия (ограничение на перемещение некоторых точек тела) остаются справедливыми для вектора перемещения
, причем кинематические краевые условия (ограничение на перемещение некоторых точек тела) остаются справедливыми для вектора перемещения 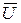 , так и для его вариации. При малых деформациях объем, по которому производится интегрирование, можно считать неизменным и поменять местами символы интегрирования и варьирования. Если выполняется обобщенный закон Гука, то подынтегральное выражение есть квадратичная форма по компонента деформации:
, так и для его вариации. При малых деформациях объем, по которому производится интегрирование, можно считать неизменным и поменять местами символы интегрирования и варьирования. Если выполняется обобщенный закон Гука, то подынтегральное выражение есть квадратичная форма по компонента деформации:
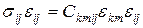 , тогда
, тогда
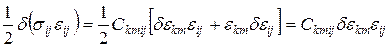
Работа внутренних сил:
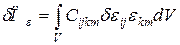
Элементарную работу внутренних сил для упругого тела отождествляют с потенциальной энергией деформированного состояния. Если к телу приложены внешние, массовые, поверхностные и сосредоточенные силы, то они совершают работу на перемещение точек, лежащих внутри тела и на его границах. Если задана кинематически допустимая вариация 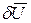 , то элементарная работа внешних сил вычисляется по формуле:
, то элементарная работа внешних сил вычисляется по формуле:
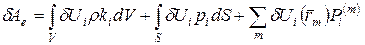
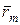 - Радиус вектор точек приложении сосредоточенных сил
- Радиус вектор точек приложении сосредоточенных сил 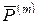 .
.
Если пренебречь эффектами выделения тепла при дифференцировании, то элементарные работы внешних сил и внутренних сил равны между собой. Тогда вариационное уравнение примет вид:
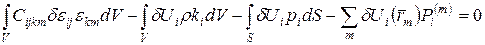
Представленная общая форма принципа возможных перемещений может быть модифицирована путем принятия некоторых кинематических и статических гипотез. В частности для стержней гипотеза Бернулли приводит к тому, что из всех слагаемых, определяющих потенциальную энергию деформаций, ненулевым становится только одно, определяющее деформацию растяжения / сжатия волокон, параллельных оси стержня. В связи с тем, что принятие этой гипотезы приводит к линейному распределению перемещений по площади конечного сечения, а также к линейному распределению деформаций, то можно вычислить интегралы по площади поперечного сечения. Тогда вариационное уравнение будет содержать только интеграл по длине стержня:
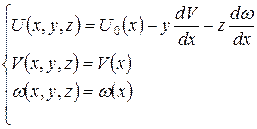
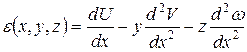
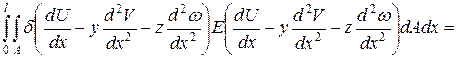
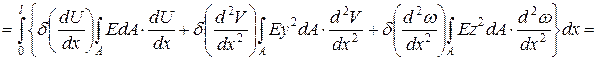
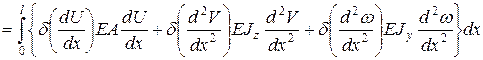
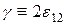
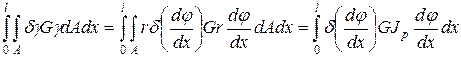
Все слагаемые с поперечными координатами в 1-ой степени и их произведения уничтожаются при интегрировании, т.к. Выбранная СК – главная центральная система поперечного сечения.
В теории стержней помимо сосредоточенных сил рассматриваются сосредоточенные моменты. Дополним выражение вариационного принципа возможной работой сосредоточенных моментов.
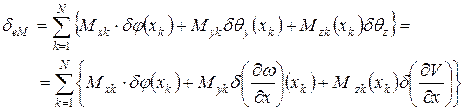
Принцип возможных перемещений для стержня следует записать в виде: 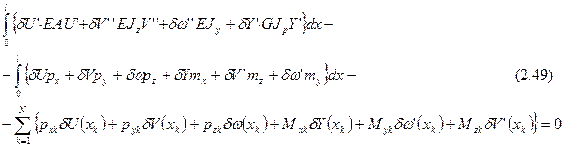
В (2.49) 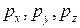 - компоненты нагрузки распределенной вдоль оси стержня;
- компоненты нагрузки распределенной вдоль оси стержня; 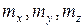 - Компоненты момента, распределенного вдоль оси стержня;
- Компоненты момента, распределенного вдоль оси стержня; 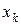 - точка приложения сосредоточенных сил и моментов.
- точка приложения сосредоточенных сил и моментов.


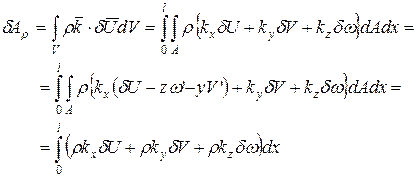
Данная формула справедлива только для случая, если компоненты массовой силы 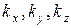 равномерно распределены по поперечному сечению с координатой х, а также при постоянной по сечению плотности.
равномерно распределены по поперечному сечению с координатой х, а также при постоянной по сечению плотности.
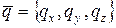
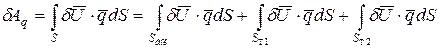
Последние два интеграла представляют собой работу сосредоточенной силы и сосредоточенного момента, которые являются главным вектором и главным моментом распределенной по торцу нагрузке q.





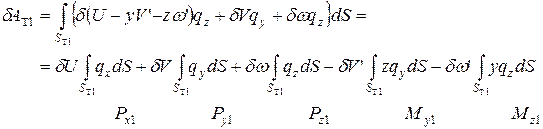
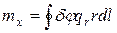
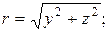
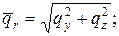
Проведенное рассуждение показывает, что распределенные по торцам нагрузки можно заменить их главными векторами, главными моментами относительно центра тяжести поперечного сечения.
Предполагаем аналогичное рассуждение для произвольного поперечного сечения с текущей координатой х и рассмотрим работу нагрузок, распределенных по боковой поверхности стержня.





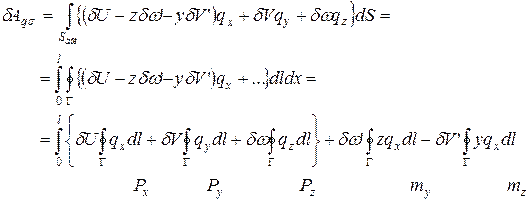
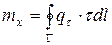
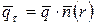 , где n вектор нормали к поперечному сечению.
, где n вектор нормали к поперечному сечению.
Распределенными изгибающими и крутящими моментами для тонких стерней обычно пренебрегают в силу малости этих величин, имеющих порядок.
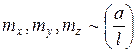
а – характерный поперечный размер стержня.
В дальнейшем при построении варианта метода КЭ для расчета стержней и стержневых систем будем использовать формулировку вариационного принципа (49), пренебрегая распределенными моментами 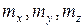 .
.
Будем рассматривать вариант МКЭ в перемещениях на основании вариационного уравнения Лагранжа. Будем считать, что конечно-элементная сетка задана, т.е. установлено соответствие между номерами узлов и номерами КЭ и определены координаты узлов. Для каждого КЭ Будем считать функции Формы так, что перемещение произвольной точки, принадлежащей КЭ однозначно определяется перемещениями его узлов.
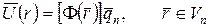 (2.50)
(2.50)
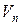 - многогранник, определяющий КЭ.
- многогранник, определяющий КЭ.
Введем в рассмотрение векторы напряжения и деформации:
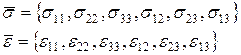 (2.51)
(2.51)
так, что произведение этих двух векторов дает работу
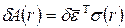
Запишем закон Гука в матричной форме, заменив тензоры второго ранга по (51), а тензор 4-го ранга упругих постоянных – квадратной матрицей 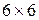 .
.
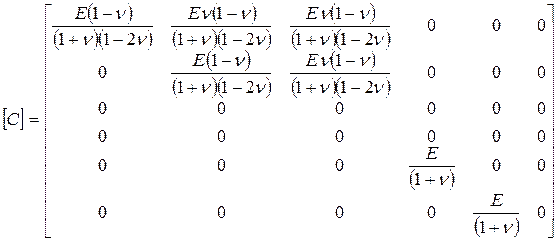 (2.52)
(2.52)
Для произвольного анизотропного материала матрица закона Гука будет заполнена; для ортотропного материала при выборе СК, совпадающей с главными осями анизотропии, матрица будет иметь такую же структуру как (52), но ее компоненты будут вычисляется через 9 независимых постоянных ортотропного материала.
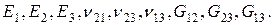
Абронова
Так как стержни образуют плоскую систему, но их оси ориентированы по-разному, то следует каждому узлу приписать две степени свободы:
1. продольное перемещение
2. поперечное перемещение
При этом поперечное перемещение не должно влиять на деформацию стержня.
3.) Описываем матричные характеристики
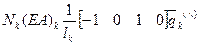
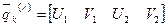
 |  |
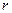
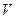
1 2 
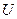
В локальных координатах:
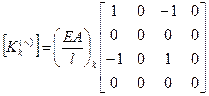
Для перехода из локальных координат в глобальные необходима матрица направляющих косинусов.
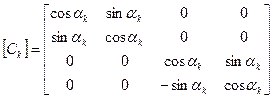
В глобальных координатах матрица жесткости имеет вид:
Так как нагрузки приложены только по узлам стержневой системы, то вычисление вектора узловой нагрузки КЭ не требуется.
4.) Сетка конечных элементов.
5.) Составление матрицы связи.
| ||
|
I:
2: Список закрепленных узлов:
| № узла | Код 1 | Код 2 |
B:
| 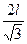
| 
|
| 
| 
|
| 
| 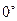
|
6.)Матричные характеристики ансамбля КЭ-ов.
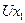
| 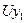
| 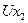
| 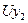
| 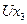
| 
| |
| 
| 
| 
| 
| ||
| 
| 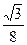
| 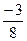
| 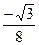
| ||
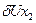
| -1 | |||||
| ||||||
| 
| 
| -1 | 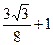
| 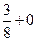
| |
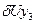
| 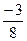
| 
| 
| 
|
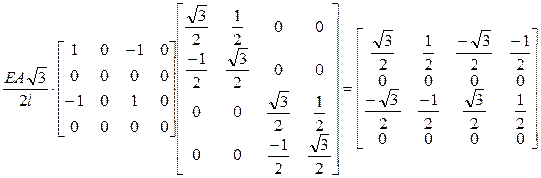
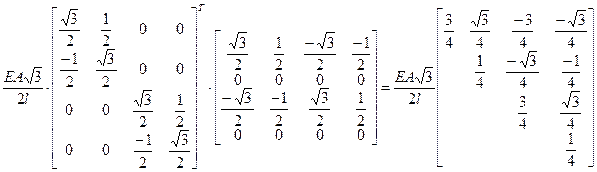
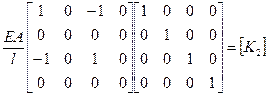
7.) Удовлетворение краевым условиям в перемещениях.

8.) Решаем систему уравнений
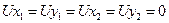
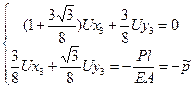







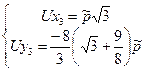
9.) Вычисление узловых сил (усилий в стержнях)
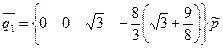 - в глобальных координатах
- в глобальных координатах
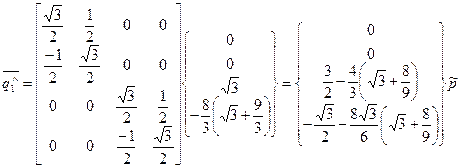
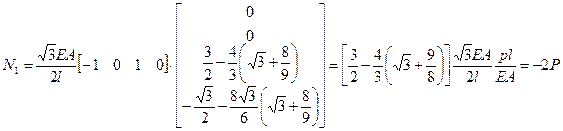
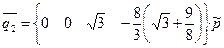 - глобальные (они же локальные) координаты
- глобальные (они же локальные) координаты
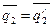
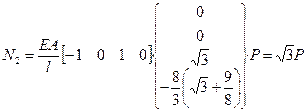



 3
3 
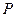
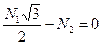
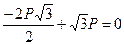 0=0
0=0
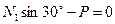
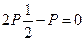 0=0
0=0
Дата добавления: 2015-02-16; просмотров: 2052;
