Моделирование стержневых систем методом конечных элементов

В методе конечных элементов основной идеей является замена исходной непрерывной системы (деформированного тела) множеством связанных математических точек. Будем считать, что определена неподвижная система координат (глобальные координаты), по отношению к которой определяется движение мат. точек. В дальнейшем будем называть узлами мат. токи принадлежащие деформированному твердому телу, для которых указаны начальные координаты и нумерация, причем каждая точка имеет уникальный номер. Количество таких точек будем считать конечным.

Некоторое множество этих точек принимаем за вершины многогранника, причем множество всех возможных многогранников определенное на множестве узлов отличается тем, что многогранники не пересекаются между собой и полностью заполняют объем тела. Последнее требование может быть ослаблено в близи границ тела. В том смысле, что грань многогранника, вершины которой принадлежат поверхности может не принадлежать поверхности тела.

Такие многогранники, каждому из которых приписаны уникальные номера называются конечными элементами (КЭ). Если установлено однозначное соответствие между номерами многогранников и номерами узлов, которые являются их вершинами, то говорят, что определена сетка КЭ. Переход от непрерывного тела к его конечно-элементной модели осуществляется путем выбора способа определения некоторой искомой функции в произвольной точке объема по ее значению в узлах. Функция которая осуществляет эту интерполяцию называется функцией формы. Основное отличие метода КЭ от других численных методов заключается в том, что интерполяция осуществляется только по узлам принадлежащим КЭ.

Функции формы реализующие кусочную интерполяцию разделяют следующим образом:

1. Функции формы должны принадлежать множеству функций, интегрируемых в пределах КЭ.

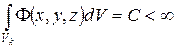
2. Функции формы с определенным номера k должна принимать значение =1 в этом узле и =0 во всех других узлах.

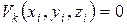
3. Функция формы должна быть однозначной в пределах объема КЭ.

Если производится интерполяция в пределах некоторой функции, для которой не выполняется условие 2, но выполняется условие 1 и 3, то эту так называемую аппроксимирующую функцию следует нормировать составляя систему уравнений вида

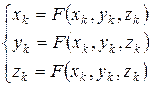
Для определения значений функции в узлах в рамках МКЭ используются различные функционалы, минимум которых соответствует реальному значению исходной функции. Таким функционалом может быть невязка между строгим решением уравнения равновесия и приближенным решением; невязка между значением функции на границе и заданными краевыми условиями: Вариационный функционал Лагранжа (принцип возможных перемещений), вариационный функционал Костельяна (принцип минимума дополнительной работы) и т.д.

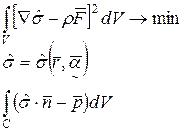
Выбор вариационного функционала определяет модификацию метода КЭ. Если используются функционалы невязки между значениями функции на границе или некоторыми дифференциальными операторами над ней в объеме, то МКЭ можно считать дискретным вариантом метода Бубнова - Галеркина. Если используется функционал Лагранжа, то МКЭ можно трактовать как вариант метода Ритца.