Применение метода начальных параметров

Запишем уравнение состояния при статических нагрузках для однородного участка стержня:

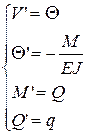
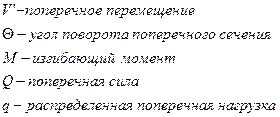
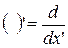
Т.к. q является известной функцией координаты х, то систему уравнений можно проинтегрировать.

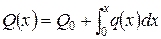
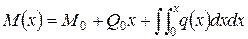
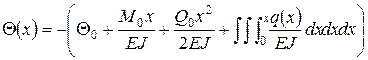
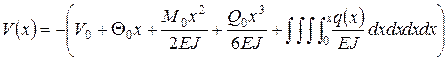
Для применения метода начальных параметров вводим вектор состояния в виде:

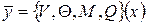(2.35)

Решение дифференциального уравнения запишем в матричной форме:

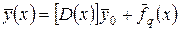(2.36)

Вид матрицы влияния D следующий:

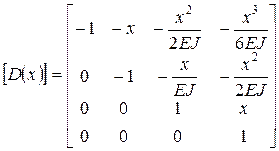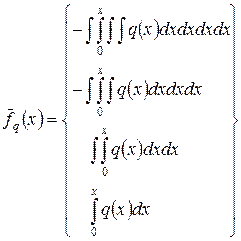; (2.37)

Если для стержня заданы начальные условия: Вектор 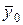и распределенная нагрузка q, то вектор состояния в любой точке определяется формулой (36).

Пусть стержень состоит из нескольких участков, границы которого определяются также как в методе сечений.

0 1 2 3 n – 1 n

l₁ l₂ l₃ l_n

Точки – границы участков, будем называть узлами и нумеровать их от 0 до n.

Участки будем различать по индексу, который представляет собой либо номер крайнего правого узла, либо номера левого и правого узлов.

Рассмотрим участок с номером k. Для него справедлива формула (2.36), в которой начальный вектор состояния 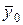должен иметь индекс .

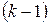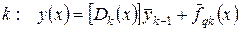
Индекс у матрицы D обозначает, что при ее вычислении в (37) подставляются параметры, соответствующего участка, а именно жесткость стержня EJ и распределенная нагрузка q.

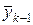- начальное условие для участка с номером k.

Получим из (2.36), в котором текущая переменная x заменена координатой конца 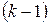участка.

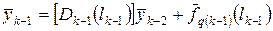
Для 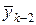можем записать аналогичное выражение:

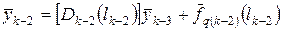
Очевидно, что этот процесс можно продолжать до тех пор, пока индекс начальных условий не примет значение 0.

Тогда для участка с номером k можно исключить переменные 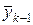, 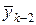и т.д. через вектор состояния в узле с номером 0, который в дальнейшем будет называться вектором начальных параметров.

Проводя такое исключение получим:

(2.38)

Введем обозначения:

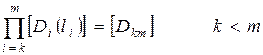(2.39)

Матрица 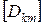в дальнейшем будет называться матрицей влияния узла k на узел m.

С учетом этого обозначения (38) можно записать короче:

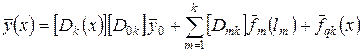(2.40)

Пользуясь формулой (40), найдем состояние в последнем, самом правом узле с номером n:

(2.41)

Если известны все внешние нагрузки, то формула (41) позволяет найти состояние в конце стержня по известному состоянию 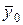, т.е. по начальным параметрам.

Пусть в узле с номером m<k приложена сосредоточенная сила 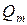. Вектор состояния, соответствующий такой силе можно записать виде:

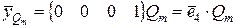
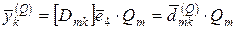(2.42)

Здесь 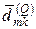обозначает 4-й столбец матрицы влияния .

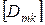По аналогии определим влияние сосредоточенного момента, приложенного в узле m.

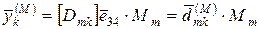(2.43)

Добавим в (40) и (41) влияние сосредоточенных нагрузок:

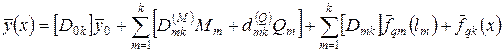(2.44)

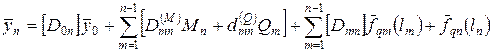(2.45)

Воспользоваться (44) можно только в том случае, если известен вектор 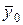, все его 4 компоненты. На самом деле, в одном узле мы можем задать только 2 компоненты. Перечислим допустимые сочетания компонент:

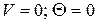1. - жесткая заделка

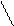
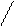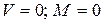2. - шарнирное попирание

3. 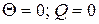- скользящая заделка

4.

Недостающих 2 начальных параметра можно определить из уравнения (2.45).

Разрешающее уравнение метода начальных параметров имеет матрицу 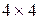, которая представляет собой матрицу влияния нулевого узла на последний. Входящий в это уравнения вектор влияния сосредоточенных моментов, сил и распределенных нагрузок известен по условию задачи. Смысл этой системы уравнений: вычисление компонент вектора состояния в последнем узле по начальным параметрам – известным нагрузкам. Из которых условий 2 начальных параметра известно и, следовательно, можно произвести матричное умножение. Получим вектор влияния известных начальных параметров на состояние конца стержня и перенести его вместе с вектором влияния нагрузок в правую часть уравнения. В результате получится система уравнений с матрицей 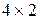, которая представляет собой матрицу влияния неизвестных начальных параметров на состояние в конце стержня. Но из 4-х компонент вектора правой части известно только 2 – т.е. которые соответствуют краевым условиям на конце стержня. Удаляя из системы 2 уравнения, соответствующих неизвестным параметрам состояния на конце стержня приходим к системе с матрицей 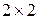относительно 2-х неизвестных начальных параметров.

Приведенный алгоритм решения задач плоского изгиба методом начальных параметров позволяет решить статически определимые задачи.

Рассмотрим модификацию алгоритма для решения статически неопределимых задач о плоском изгибе стержней с промежуточными опорами.

0 1 2 … n – 1 n

R₁ R₂

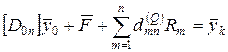
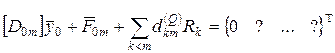
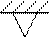
Представим, что в некоторых узлах установлены дополнительные опоры (за исключением узла 0 и узла n). Если освободиться от связей, то действие этих опор на состояние стержня заменяется их реакциями и дополнительными условиями: равенство нулю поперечных перемещений на каждой из опор. Влияние опорных реакций промежуточных опор на состояние в конце стержня учитывается слагаемым вида:

,

где как и ранее 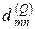- вектор влияния сосредоточенной силы, приложенной в узле m на узел n (т.е. 4-ий столбец матрицы );

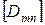- абсолютная величина опорной реакции (пока неизвестная).

Т.о. разрешающая система уравнений будет содержать 4 начальных параметра и N неизвестных опорных реакции. Для замыкания этой системы привлекаем условие = 0 поперечного перемещения на каждой из N промежуточных опор. С этой целью записываем уравнение влияния начальных параметров внешних нагрузок и промежуточных опор на узел m, для которого формулируется условие отсутствие поперечного перемещения.

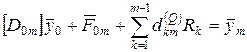
Перемещение в узле m определяется 1-ой строчкой этого уравнения. Обозначим ее

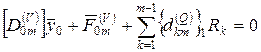
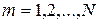(2.46)

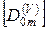- матрица строка из 4-х элементов;

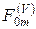- 1-ая компонента вектора влияния внешних нагрузок;

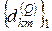- 1-ая компонента 4-го столбца матрицы влияния узла k на узел m.

Для организации вычислений при большом количестве участков и промежуточных опор удобно реализовать метод начальных параметров на ЭВМ. С этой целью рассмотрим составление разрешающей системы уравнений в матричной форме с измененной нумерацией компонент вектора начальных параметров.

Пусть вектор начальных параметров разбит на 2 части:

1. Соответствует компонентам, заданным в начале стержня.

2. Неизвестным компонентам начального состоянии.

1. Жесткая заделка:

0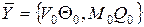

2. Шарнирно-неподвижная опора

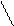
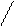0

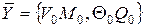
3. 0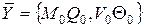

Подобное изменение порядка следования начальных параметров эквивалентно перестановке столбцов матрицы влияния 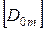. Обозначим матрицу с переставленными столбцами через 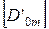. Аналогичную операцию производим с вектором , но перестановки выполним собирая известные и неизвестные компоненты состояния на конце стержня.

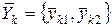
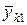- известные компоненты;

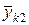- неизвестные компоненты.

Такая перестановка компонент, состояния эквивалентна перестановке строк в матрице 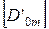, векторах влияния известной нагрузки и промежуточных опор.

Обозначим 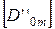, , 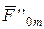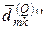- Соответствующие матрицы и векторы с переставленными строками.

Тогда разрешающую систему удобно записать в клеточной форме:

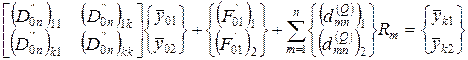
Нижний блок системы уравнений следует удалить, т.к. вектор 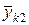неизвестный. Умножая матрицу в оставшемся уравнении, получаем:

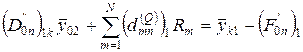(2.47)

Дополнительное условие запишем следующим образом:

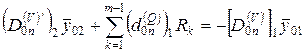(2.48)

(2.48): 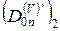- элементы строки матрицы влияния 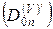соответствующие неизвестным начальным параметрам. (3 и 4 элемент). В правой части - оставшиеся элементы этой строки. Система уравнений (2.47) и (2.48) содержит (N+1) неизвестных – 2 начальных параметра вектора 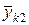и n промежуточных опорных реакций.