Алгоритм построения интервальных оценок параметров регрессионной модели в Excel.

Алгоритм построения доверительных интервалов параметров модели имеет следующую последовательность:

1) оценка параметров модели по выборочным данным производится с помощью функции ЛИНЕЙН при параметрах :Константа =1 (=0, если нет свободного члена), статистика =1(всегда). Эти вычисления будут равноценным вычислениям по формулам ; .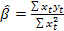

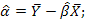
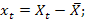
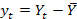2) оценка значений эндогенной переменной и вычисление остатков регрессии: основываясь на данных, полученных с помощью функции линейн подставляем и рассчитываем 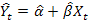; 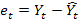, t=1,…,n;

3) оценка дисперсии возмущений, так же получается при применении функции ЛИНЕЙН (в таблице EXCEL находится под данными ско оценки первого регрессора (константы при единичном регрессоре)):данные равносильны вычисляемым по формуле ;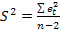

4) оценка дисперсии коэффициентов, так же выводится в функции ЛИНЕЙН под оценками параметров модели. Равносильно квадратному корню из: ;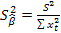

5) выбор критического (табличного значения) статистики tkp(n - 2) Критическое значение t^ статистики Стьюдента можно определить в Excel, в категории «Статистические», при помощи функции «Стьюдраспобр». Параметры функции: вероятность (уровень значимости), число степеней свободы (для парной регрессии n - 2).;

6) вычисление границ доверительных интервалов параметров модели по формулам

;

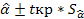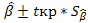
20. Проверка значимости оценок параметров линейной регрессионной модели.

При проверке качества спецификации парной регрессии наиболее важной является задача установления наличия линейной зависимости между эндогенной переменной и регрессором модели. С этой целью проверяется значимость оценки параметров α и β. В процедуре проверки значимости оценки параметра парной регрессии используется дробь Стьюдента 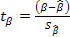которая при истинности гипотезы H0:β = 0, против конкурирующей H1: β 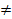0, принимает вид: 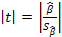,и, при выполнении условий Гаусса—Маркова (относительно случайных возмущений), имеет t-распределение с числом степеней свободы n-2. Аналогично формируется t-статистика для проверки гипотезы H0 значимости параметра α, однако параметр β в парной регрессии имеет более важную роль, так как его значимость соответствует значимости регрессора и наличию линейной связи между переменными модели.

Алгоритм проверки значимости параметра β выполняется в следующей последовательности:

1) оценка параметров парной регрессии;

2) оценка дисперсии возмущений S²;

3) оценка 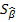ско оценки параметра β;

4) выбор значения tкр (по заданному уровню значимости α и числу степеней свободы (n - 2) из таблиц распределения Стьюдента);

5) проверка неравенства 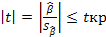, при H0: β=0

Если данное неравенство выполняется, то регрессор признается незначимым, если не выполняется, то гипотеза H0: β=0 отвергается и регрессор признается значимым, т. е. между эндогенной переменной и регрессором присутствует линейная зависимость.

При проверке статистической значимости параметров модели можно использовать следующее приближенное правило

1) 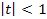, то коэффициент не может быть признан значимым (доверительная вероятность меньше 0,7);

2) 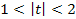, то коэффициент может быть признан значимым с доверительной вероятностью в диапазоне между 0,7-0,95;

3) 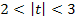, то коэффициент признается значимым с доверительной вероятностью в диапазоне между 0,95-0,99;

4) , то значимость коэффициента очевидна (доверительная вероятность находится в диапазоне между 0,99 и выше).

Чем больше объем выборки, тем надежнее выводы о значимости коэффициента. При n > 10 приближенное правило дает результаты, близкие к табличным.