Основные числовые характеристики вектора оценок параметров классической регрессионной модели.

Теорема Гаусса—Маркова. Пусть матрица X имеет полный ранг. При выполнении условий Гаусса—Маркова МНК-оценки параметров а, b относятся к классу линейных по Y, несмещенных оценок с минимальной дисперсией.

a) Вектор оценок параметров 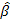=(X^TX)^-1X^TY=AY, где размерность А=(k,n)

b) Математическое ожидание E= 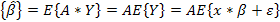=Axβ=I_k*β=β.

Оценка называется эффективной, если она удовлетворяет критерию E( ( (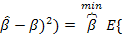

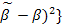
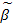- альтернативная оценка, полученная по выборке того же объема.

Эффективность несмещенных оценок

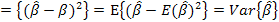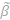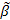Критерий эффективности: E = min(по )Var{ }. Несмещенная оценка называется эффективной, если она имеет минимальную дисперсию по сравнению с другими оценками в классе выбранных процедур,

c) Автоковариационная матрица вектора оценок параметра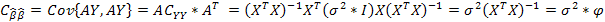

Оценка автоковариационной матрицы: Оценка дисперсии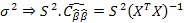

Несмещенная оценка дисперсии возмущений: 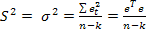, где (n-k)число степеней свободы.

Выводы:МНК оценки параметров являются: а) несмещенными, б) линейными, в) эффективными, по теореме Гауса-Маркова.