F-тест качества спецификации парной линейной регрессионной модели
F-тест - оценивание качества уравнения регрессии - состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fвыч и критического (табличного) Fкрит значений F-критерия Фишера. Fвыч определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы.
Коэффициент детерминации является случайной величиной (так как вычисляется по выборочным данным), и для оценки его статистической
значимости, в соответствии со стандартной процедурой, следовало бы
сравнить его вычисленное значение с табличным (критическим). Однако
таблиц распределения коэффициента детерминации не существует, поэтому для проверки статистической гипотезы о значимости R2 используется косвенный метод: вычисляется некоторая вспомогательная статистика с известным распределением; проверяется гипотеза ее статистической значимости; устанавливается взаимосвязь между вспомогательной статисткой и коэффициентом детерминации; на основании этой взаимосвязи делается вывод о статистической значимости коэффициента детерминации. Для составления вспомогательной статистики рассмотрим две случайные величины U и V. Статистика U имеет распределение х2 (хи-квадрат)
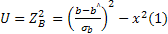 (1)
(1)
так как случайная величина 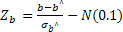 , как было показано выше, имеет стандартное нормальное распределение, а ее квадрат можно рассматривать как сумму квадратов стандартных нормальных величин, включающую только одно слагаемое.
, как было показано выше, имеет стандартное нормальное распределение, а ее квадрат можно рассматривать как сумму квадратов стандартных нормальных величин, включающую только одно слагаемое.
В качестве второй вспомогательной статистики, имеющей распределение х2 с параметром, равным числу степеней свободы n - 2, используется статистика вида:
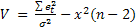 (2)
(2)
Статистика F, как легко проверить, совпадает с квадратом f-статистики для параметра b:
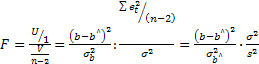 =
= 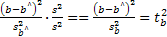
и имеет распределение Фишера с параметрами v1=1,v2=n-2 (n— объем выборки):
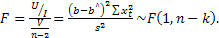 (3)
(3)
Для проверки гипотезы Н0:b = 0 статистика (3) принимает вид:
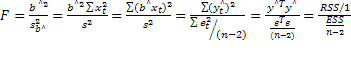 .
.
Связь между статистиками F и R2для случая парной регрессии
(k=2) имеет вид:
F= 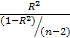 (4)
(4)
Справедливость (4) проверяется непосредственно:
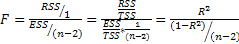 (5)
(5)
Таким образом, как следует из формулы (5), F = 0 в том случае, если R2=0. Поэтому, проверяя значимость F статистики (сравнивая ее вычисленное по выборочным данным значение с табличным), мы можем проверить статистическую значимость коэффициента детерминации. ЕслиFвыч<Fкр, то принимается нулевая гипотеза H0:b = 0 и, следовательно, коэффициент детерминации незначим, в противном случае нулевая гипотеза отвергается и коэффициент детерминации признается статистически значимым.
Дата добавления: 2015-01-10; просмотров: 6729;
