Спецификация множественной линейной регрессионной модели.

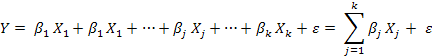
k-число параметров модели

X_j – j-й регрессор, j=1,…,k

Y-эндогенная переменная

β_j – j-й параметр модели j=1,…,k

ε – случайное возмущение

Матричная форма:

Y=βX+ε

Y = (Y₁, Y₂, …, Y_n) – вектор-столбец значений эндогенной переменной

X = 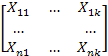– детерминированная матрица регрессоров полного ранга (rank(X)=k)

Через X₁ = (X_11, X_12,…, X_n1)^T = I обозначен единичный вектор-столбец, позволяющий включить в число регрессоров постоянный член и формализовать спецификацию модели со свободным членом и без него в единообразной форме.

β = (β_1, β_2,…, β_k)^T- вектор-столбец параметров модели

ε= (ε_1, ε_2,…, ε_n)^T – вектор-столбец случайных возмущений